The time period of a simple pendulum, in the form of a hollow metallic sphere, is T. When it is filled with sand and mercury, then its time periods are T1andT2 respectively. When it is partially filled with sand then its time period is T3. The correct relation between T1,T2&T3 will be
T=T1=T2=T3
T=T1=T2<T3
T=T1>T2>T3
T>T1>T2=T3
The correct Answer is:B
To solve the problem, we need to analyze how the time period of a simple pendulum changes when the mass distribution of the pendulum changes. The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where:
- L is the distance from the pivot point to the center of mass of the pendulum,
- g is the acceleration due to gravity.
Step 1: Understanding the Initial Time Period T
For the hollow metallic sphere, the center of mass is at its midpoint. The time period is given as T.
Step 2: Time Period When Filled with Sand T1
When the hollow sphere is filled with sand, the center of mass will still be at the center of the sphere (since sand fills it uniformly). Therefore, the effective length L remains the same, and thus:
T1=T
Step 3: Time Period When Filled with Mercury T2
Similarly, when the hollow sphere is filled with mercury, which is denser than sand, the center of mass is still at the center of the sphere. Thus, the effective length L remains unchanged, and we have:
T2=T
Step 4: Time Period When Partially Filled with Sand T3
When the hollow sphere is partially filled with sand, the center of mass shifts downward. This means that the effective length L increases. Since the time period is directly related to the square root of the effective length, we can conclude that:
T3>T
Step 5: Establishing Relationships
From the above analysis, we can summarize the relationships as follows:
- T1=T
- T2=T
- T3>T
Thus, since T1 and T2 are equal and both are less than T3, we can write the final relationship as:
T1=T2<T3
Final Relation
The correct relation between T1,T2, and T3 is:
T1=T2<T3
- L is the distance from the pivot point to the center of mass of the pendulum,
- g is the acceleration due to gravity.
- T2=T
- T3>T
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EVALUATE YOURSELF - 4
8 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - C. U . Q
75 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EVALUATE YOURSELF - 2
4 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
The graph of time period (T) of a simple pendulum versus its length (I) is
View SolutionA mass is suspended separately by two different springs in successive order, then time periods is t1andt2 respectively. It is connected by both springs as shown in fig. then time period is t0. The correct relation is
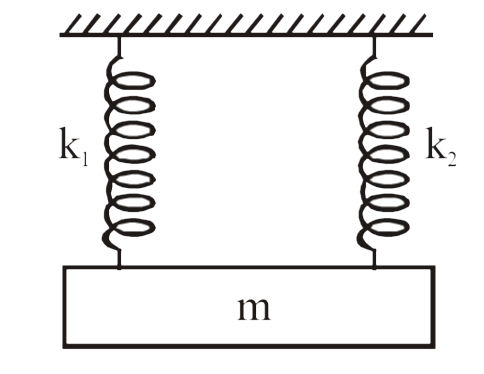
View Solution
Knowledge Check
The graph of time period (T) of simple pendulum versus its length (l) is
A B
B C
C D
D
The time period of a simple pendulum at the surface of the earth is T. If it is taken to a height of 640 km, its time period will
Aincrease by 20%Bincrease by 10%Cdecrease by 10%Ddecrease by 5%The time period of a simple pendulum whose bob is a hollow sphere is T. The period is T1 where the bob is filled with sand, T2 where it is filled with mercury and T3 when it is half filled with mercury Which of the following is true?
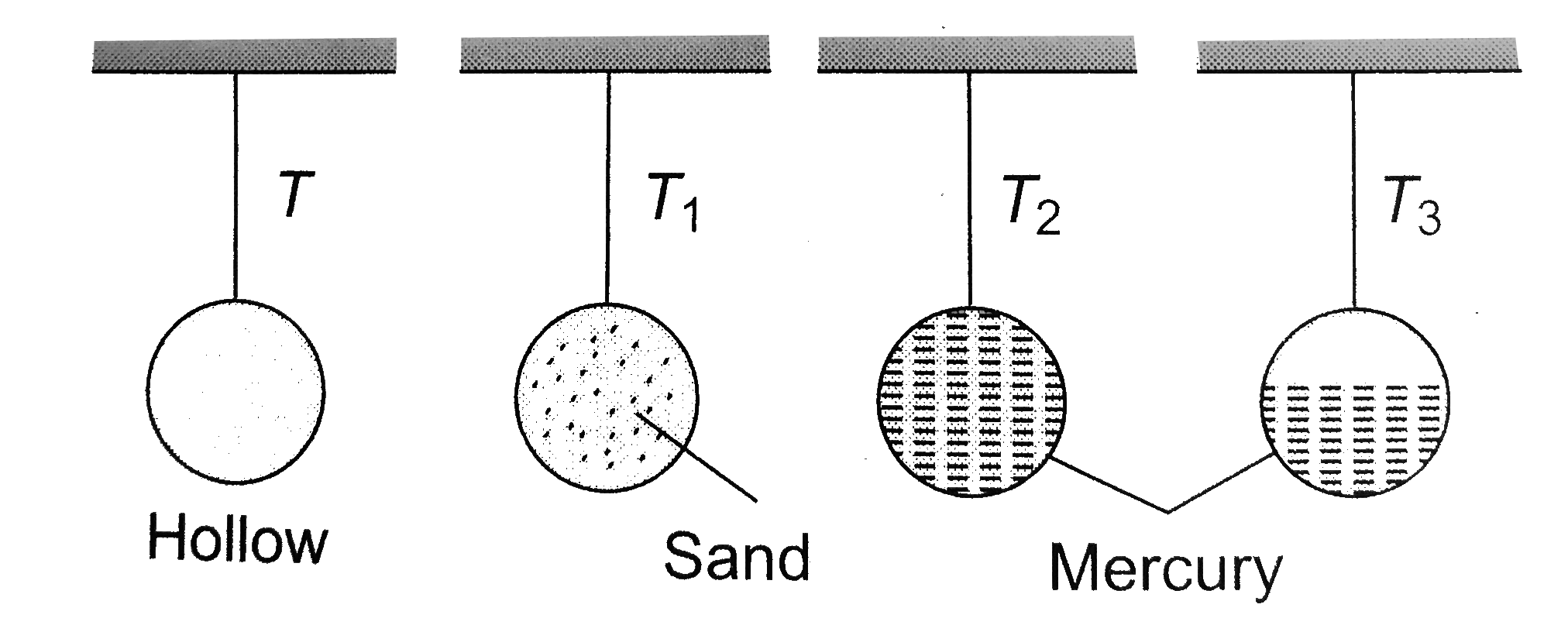 AT=T1=T2>T3BT1=T1=T3>TCT>T3>T1=T2DT=T1=T2<T3
AT=T1=T2>T3BT1=T1=T3>TCT>T3>T1=T2DT=T1=T2<T3
T0 is the time period of a simple pendulum at a place. If the length of the pendulum is reduced to 116 times of its initial value, the modified time period is :
View SolutionThe time period of simple pendulum is T. If its length is increased by 2%, the new time period becomes
View SolutionA mass is suspended separately by two different springs in successive order then time periods is t1 and t2 respectively. If it is connected by both spring as shown in figure then time period is to, the correct relation is
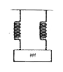
View SolutionTime period of a pendulum on earth surface is T1. It is arranged on earth surface at a height R and thus its time period is T2. What is the ratio of T1 and T2?
View SolutionA simple pendulum is oscillating in a lift. If the lift is going down with constant velocity, the time period of the simple pendulum is T1. If the lift is going down with some retardation its time period is T2, then
View Solution
