If the velocity of a particle is v=At+Bt2, where A and B are constant, then the distance travelled by it between 1s and 2s is :
1) 23A+73B
2) A2B3
3) 32A+4B
4) 3A+7B
The correct Answer is:A
Velocity of the particle is V=At+Bt2
dsdt=At+Bt2,∫ds=∫ (AT+Bt2)dt
Therefores=(At⋅22+B(t33+C
s(t=1s)=A2+B3+C,s(t=2s)=2A+83B+C
Required distance =s(t=2s)=2A+(8)/(3)B+C<br>=(2A+(8)/(3)B+C)-((A)/(2)+(B)/(3)+C)=(3)/(2)A+(7)/(3)B
Similar Questions
The instantaneous velocity of a particle moving in a straight line is given as v=αt+βt2, where α and β are constants. The distance travelled by the particle between 1s and 2s is :
View SolutionThe velocity of a particle varies with time as per the figure shown. The distance travelled by the particle in 10 seconds is ?(m/s)
View Solution
Knowledge Check
If the velocity of a particle is v=At+Bt2, where A and B are constant, then the distance travelled by it between 1s and 2s is :
A32A+4BB3A+7BC32A+73BDA2+B3the velocity of a particle varies with time as shown below the distance travelled by the travelled by the particle during t=2s"and" t= 6s. Is
 A2πmB(2π+40)mC4πmD40m
A2πmB(2π+40)mC4πmD40m. If the velocity of a particle is (10 + 2 t 2) m/s , then the average acceleration of the particle between 2s and 5s is
A2m/s2B4m/s2C12m/s2D14m/s2
If velocity of a particle is v=bs2 ,where b is constant and s is displacement. The acceleration of the particle as function of s is?
View SolutionThe momentum of a particle is P=A+Bt2 . Where , A and B are constant perpendicular vectors . The force acting on the particle when its acceleration is at 45∘ with its velocity is
View SolutionThe variation of velocity of a particle moving along a straight line is as shown in the figure given below. The distance travelled by the particle in 5 s is
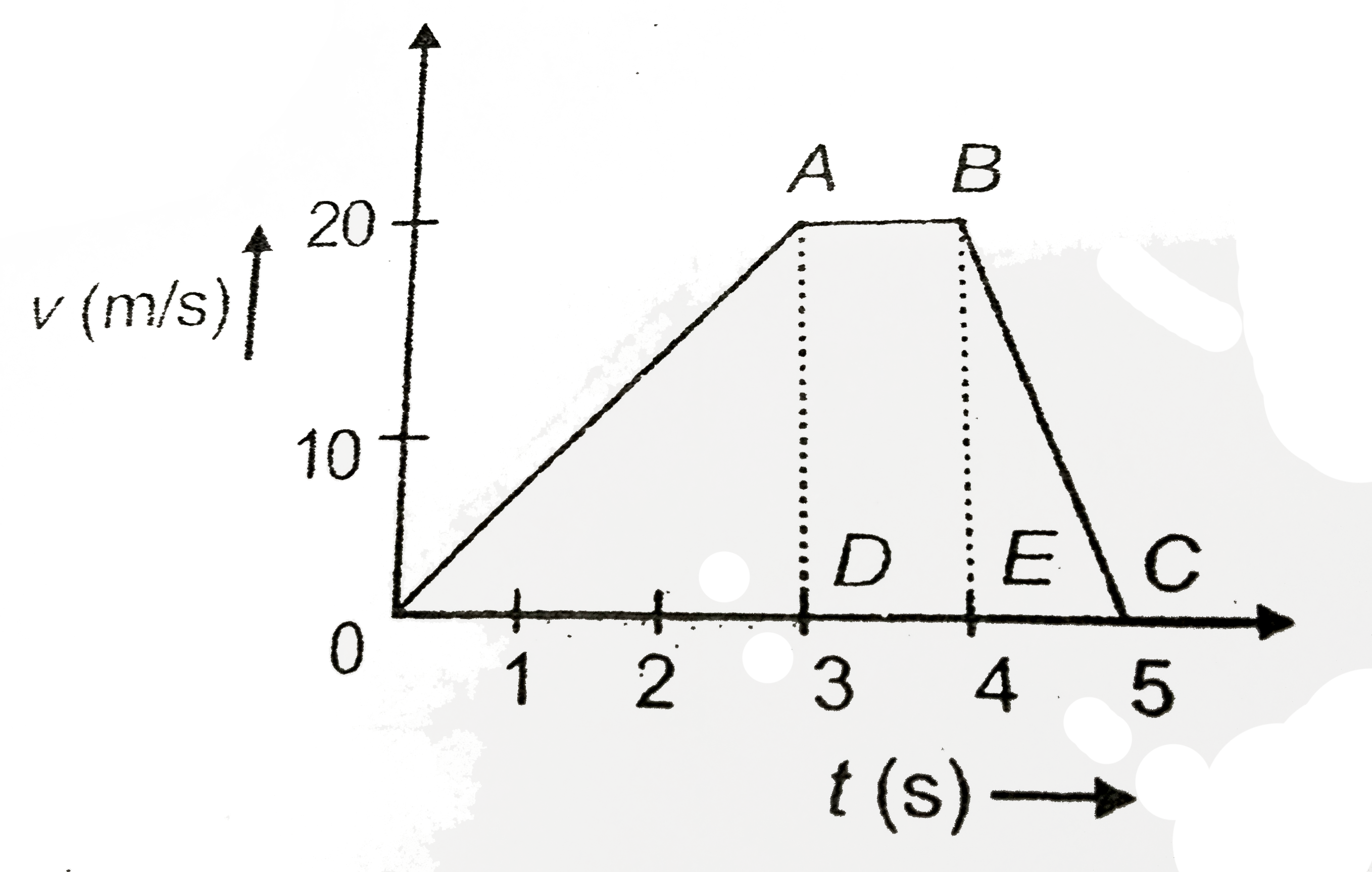
View SolutionIf the velocity of a particle "v" as a function of time "t" is given by the equation,v=a(1-e^(-bt) ,where a and b are constants,then the dimension of the quantity a^2*b^3 will be
View SolutionThe variation of velocity of a particle moving along straight line is shown in the figure. The distance travelled by the particle in 4 s is
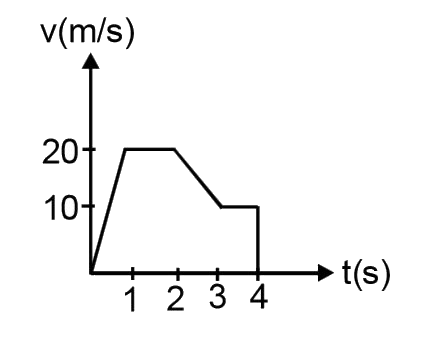
View Solution
