A mixture consists of two radioactive materials A1 and A2 with half-lives of 20s and 10s respectively. Initially the mixture has 40g of A1 and 160g of a2. The amount the two in the mixture will become equal after
60s
80s
50s
40s
The correct Answer is:D
Let after t s amount of the A1andA2 will become equal in the mixturer.
As N=N0(12)n
where n is the number of half-lives
For A1,N1=N01(12)
For A2,N2=N02(12))t/10
According to question, N1=N2
402t/20=1602t/10
2t/10=4(2t/20)or2t/10=222t/20
2t/10=2(t20+2)
t10=t20+2ort10−t20=2
ort20=2ort=40s
Topper's Solved these Questions
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - EXERCISE-4
44 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - EXERCISE-2 (H.W)
9 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE- 4 One or more than one correct answer type
13 Videos
Similar Questions
In a radioactive decay processthe activity is defined as A = - (dN)/dtwhereN(t)istheνmberofradioactiveνc≤iattimet.Tworadioactivesources,S_1andS_2havesameactivityattimet=0.Atalatertime,theactivitiesofS_1andS_2areA_1andA_2,respectively.WhenS_1andS_2havejustcomp≤tedtheir3rdand7thhalf−lives,respectively,theratioA_1/A_2 is.
View Solution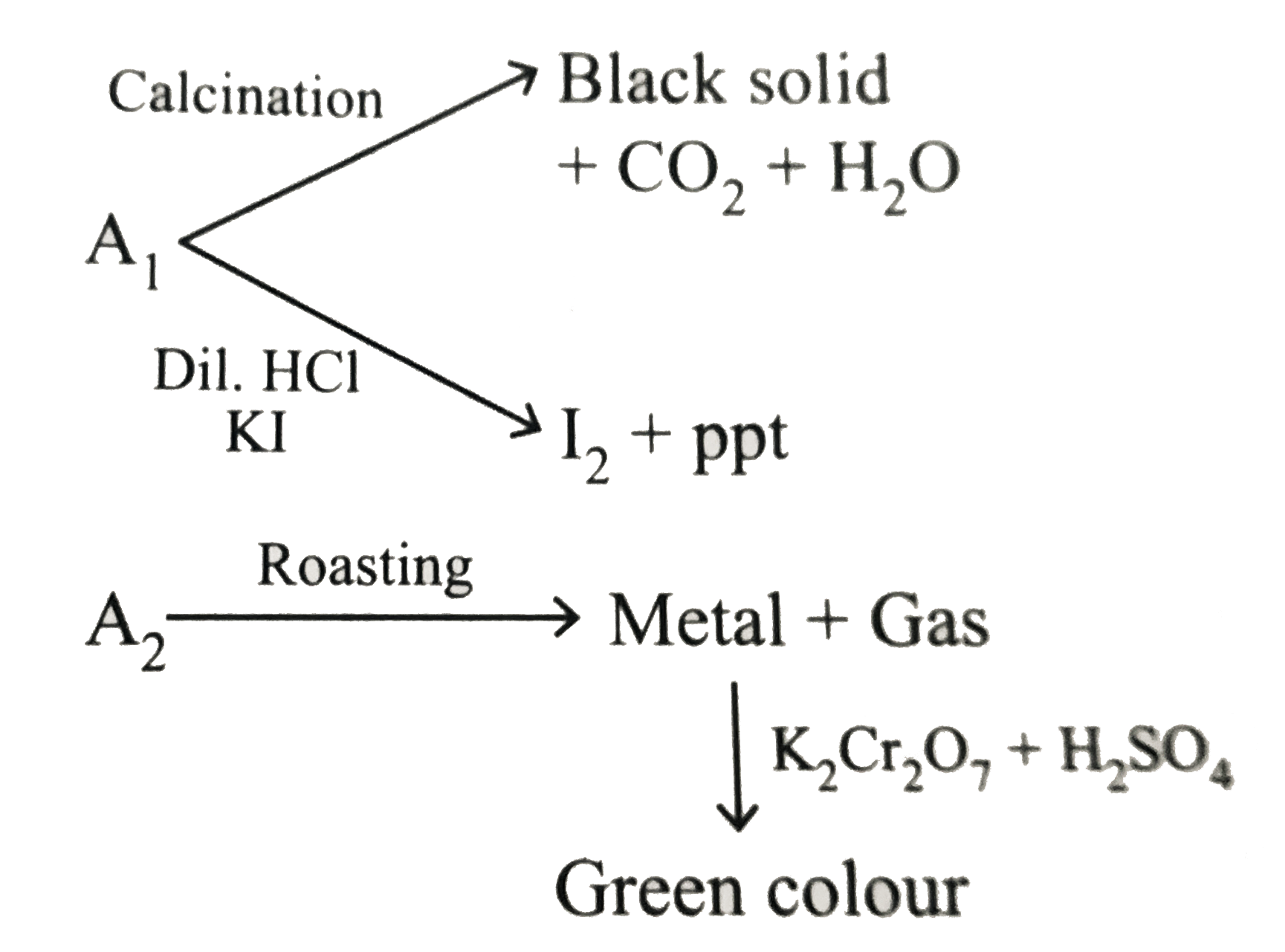
A1 and A2 are two ores of metal M.A1 on calcination gives black precipitate, CO2 and water. Identify A1 and A2.
View Solution
Knowledge Check
Atomic masses of two heavy atoms are A1 and A2. Ratio of their respective nuclear densities will be approximately
A(a) A1A2B(b) (A1A2)13C(c) (A2A1)13D(d) 1The decay constant of a radioactive isotope is λ. If A1 and A2 are its activities at time t1 and t2 respectively, then the number of nuclei which have decayed the time (t1−t2)
AA1t1−A2t2BA1−A2C(A1−A2)/λDλ(A1−A2)The ratio of nuclear density of two nuclei having mass number A1=12 and A2=14 is
A6:7B7:6C1:1D1:2
The pKa1 and pKa2 of an amino acid are 2.3 and 9.7 respectively. The isoelectric point of the amino acid is:
View SolutionTwo concentric conducting spherical shells of radii a1anda2(a2>a1) are charged to potentials ϕ1 and ϕ2, respectively. Find the charge on the inner shell.
View SolutionTwo wires of different materials of resistivity p1andp2 , length l1andl2, and area of cross-section A1andA2 respectively are connected in parallel. The ratio of current density in the two wires,j1j2 , is given by:
View SolutionThe activation energies of two reactions are Ea1 and Ea2 with Ea1>Ea2. If the temperature of the reacting systems is increased from T to T', which of the following is correct?
View SolutionThe activation energies of two reactions are Ea1 and Ea2 with Ea1>Ea2. If the temperature of the reacting systems is increased from T to T', which of the following is correct?
View Solution
