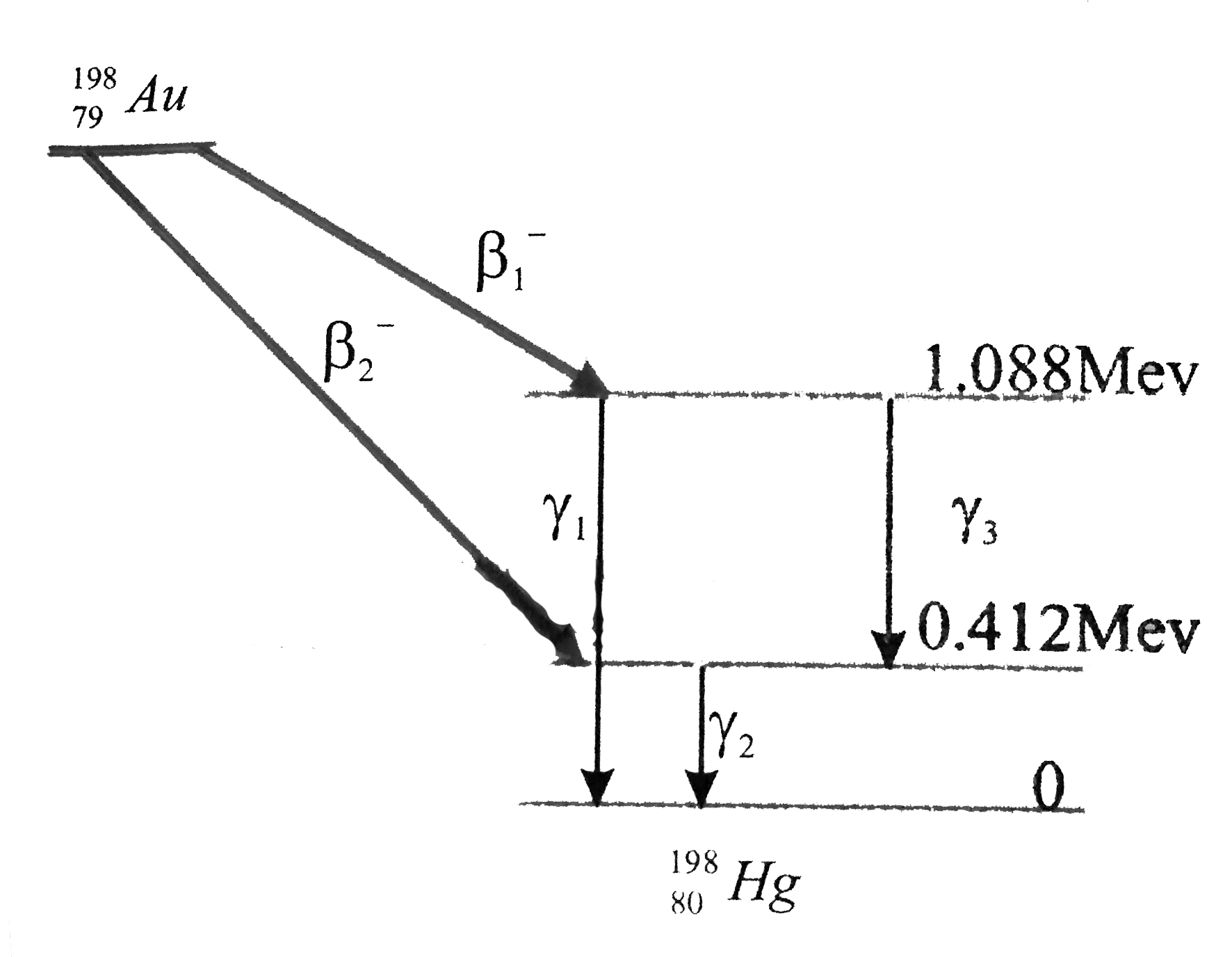
Calculate the kinetic energy of $β$ -particles and the radiation frequencies corresponding to the $γ$ -decays shown in figure.
Given, mass of $._{12} M g^{27}$ atom =26.991425 amu and mass of $._{13} A l^{27}$ atom = 26.990080 amu

Video Solution

Text Solution

Verified by Experts

Radiatin frequency of $γ_{1}$ photon=
$v_{1} = \frac{E_{3} - E_{2}}{h} = \frac{(1.015 - 0.834) M e V}{6.62 \times 10^{- 34} J s}$
$= \frac{0.18 1 \times 1.6 \times 10^{- 13} J}{6.62 \times 10^{- 34} J s} = 4.37 \times 10^{19} s^{- 1}$
Radiation frequency of $γ_{2}$ photon =
$v_{2} = \frac{E_{3} - E_{1}}{h} = \frac{(1 . 0.15 - 0) M e V}{6.62 \times 10^{- 34} J s}$
$= 2.45 \times 10^{20} s^{- 1}$
Radiation frequency of $γ_{3},$ photon =
$v_{3} = \frac{E_{2} - E_{1}}{h} = \frac{(0.834 - 0) M e V}{6.62 \times 10^{- 34}} = 2.0 \times 10^{20} s^{- 1}$
Now emission of $β_{1}^{-}$ particle is given by
$(12) M^{27 (\to_{13} A l^{27} + β^{-} + v_{2} + Q}$
$Q = [m (_{12} M g^{27}) - m (_{13} A l^{27}) - E (v_{2})$
$= [26.991425 - 26.990080] u - (E_{3} - E_{1}) M e V$
$= 0.001345 \times 9311.015 M e V$
$∴ K . E o f β_{1}^{-}$ particla $= 0.23 6 M e V$
Emission of $β_{2}^{-}$ particle is given by
$_{12} M g^{27} \to_{13} A l^{27} + β_{2}^{-} + v_{3} + Q$
$= {[26.991425 - 26.990080] 931 - 0.834} M e V = 0.418 M e V$
$∴ K . E o f β_{2}^{-}$ particle $= 0.4 18 M e V$

Updated on:21/07/2023