The focal lengths of a lens are in the ratio 8:3 when it is immersed in two different liquids refractive indices 1.6 and 1.2 respectively. The refractive index of the material of the lens i
1.25
1.5
1.8
2
The correct Answer is:D
To solve the problem, we need to find the refractive index of the lens material (μ) given the focal lengths of the lens in two different liquids and their respective refractive indices.
1. Understanding the Problem:
We are given two different liquids with refractive indices:
- Liquid 1: μ₁ = 1.6 (focal length f₁)
- Liquid 2: μ₂ = 1.2 (focal length f₂)
The ratio of the focal lengths is given as:
\frac{f₁}{f₂} = \frac{8}{3}
2. Using the Lens Maker's Formula:
The formula for the focal length of a lens in a medium is given by:
1f=μlensμmedium−1⋅1R
For our case, we can express the focal lengths as:
1f₁=μ1.6−1⋅1R=μ0.6⋅1R
1f₂=μ1.2−1⋅1R=μ0.2⋅1R
3. Setting Up the Ratio:
From the given ratio of focal lengths:
f₁f₂=83
This implies:
1/f₁1/f₂=83
Substituting the expressions for 1/f₁ and 1/f₂:
μ0.6μ0.2=83
This simplifies to:
0.20.6=83
or:
13=83
4. Cross Multiplying:
Cross multiplying gives us:
8⋅0.6=3⋅0.2
Simplifying:
4.8=0.6μ−0.2μ
This leads to:
4.8=0.4μ
5. Solving for μ:
Dividing both sides by 0.4:
μ=4.80.4=12
6. Conclusion:
The refractive index of the lens material is:
μ=12
We are given two different liquids with refractive indices:
- Liquid 1: μ₁ = 1.6 (focal length f₁)
- Liquid 2: μ₂ = 1.2 (focal length f₂)
The ratio of the focal lengths is given as:
\frac{f₁}{f₂} = \frac{8}{3}
The formula for the focal length of a lens in a medium is given by:
1f=μlensμmedium−1⋅1R
For our case, we can express the focal lengths as:
1f₁=μ1.6−1⋅1R=μ0.6⋅1R
1f₂=μ1.2−1⋅1R=μ0.2⋅1R
From the given ratio of focal lengths:
f₁f₂=83
This implies:
1/f₁1/f₂=83
Substituting the expressions for 1/f₁ and 1/f₂:
μ0.6μ0.2=83
This simplifies to:
0.20.6=83
or:
13=83
Cross multiplying gives us:
8⋅0.6=3⋅0.2
Simplifying:
4.8=0.6μ−0.2μ
This leads to:
4.8=0.4μ
Dividing both sides by 0.4:
μ=4.80.4=12
The refractive index of the lens material is:
μ=12
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (C.W)(REFRACTION THROUGH A PRISM )
Explore 8 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (C.W)(DISPERSION BY A PRISM )
Explore 4 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE-2 (C.W)(REFRACTION)
Explore 20 Videos
- NUCLEI Book:NARAYNAChapter:NUCLEI Exercise:ASSERTION & REASON
Explore 5 Videos
- SEMI CONDUCTOR DEVICESBook:NARAYNAChapter:SEMI CONDUCTOR DEVICESExercise:Level-II (H.W)
Explore 36 Videos
Similar Questions
A double convex lens has a focal length of 25 cm in air. When it is dipped into a liquid of refractive index 4/3. its focal length is increased to 100 cm. Find the refractive index of the lens material.
View SolutionA concave lens of refractive index 1.5 is immersed in a medium of refractive index 1.65. What is the nature of the lens ?
View Solution
Knowledge Check
The focal length of a glass lens in air is f. When immersed in water (refractive index μ) its focal length would be
AfB<fC>fDnothing can be decidedThe focal length of lens of refractive index 1.5in air is30cmWhen it is immersed in water of refractive index43,then its focal length will be
A120cmB60cmC30cmD240cmA convex lens is dipped in a liquid whose refractive index is equal to the refractive index of the lens. Then its focal length will
Abecome infinite.Bbecomes small but non-zero.Cremain unchanged.Dbecome zero.
A concave lens of refractive index 1.5 is immersed in a medium of refractive index 1.65. What is the nature of the lens ?
View SolutionThe radii of curvature of double convex lens are 10 cm and 20 cm respectively. Calculate its focal length when it is immersed in a liquid of refractive index 1.65. State the nature of the lens in the liquid. The refractive index of glass is 1.5.
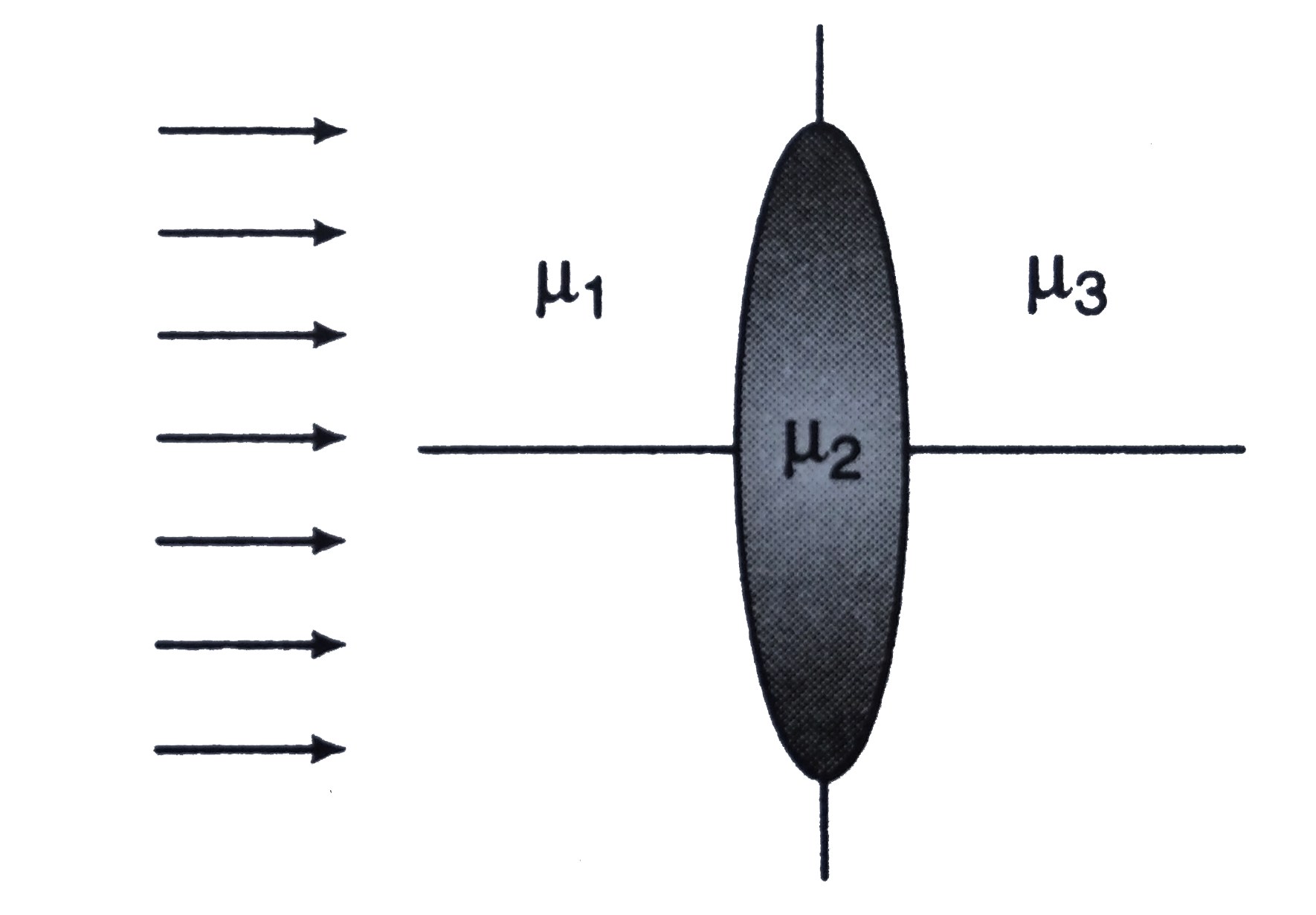
View SolutionA thin glass lens of refractive index μ2=1.5 behaves as an interface between two media of refractive indices μ1=1.4andμ3=1.6 respectively. Determine the focal length of the lens for the shown arrangement of radius of curvature of both surfaces 20cm.
View SolutionA plano-convex lens is made of refractive index of 1.6. The focal length of the lens is
View SolutionFocal length of a convex lens of refractive index 1.5 is 2 cm. Focal length of lens when immersed in a liquid of refractive index 1.25 will be
View Solution