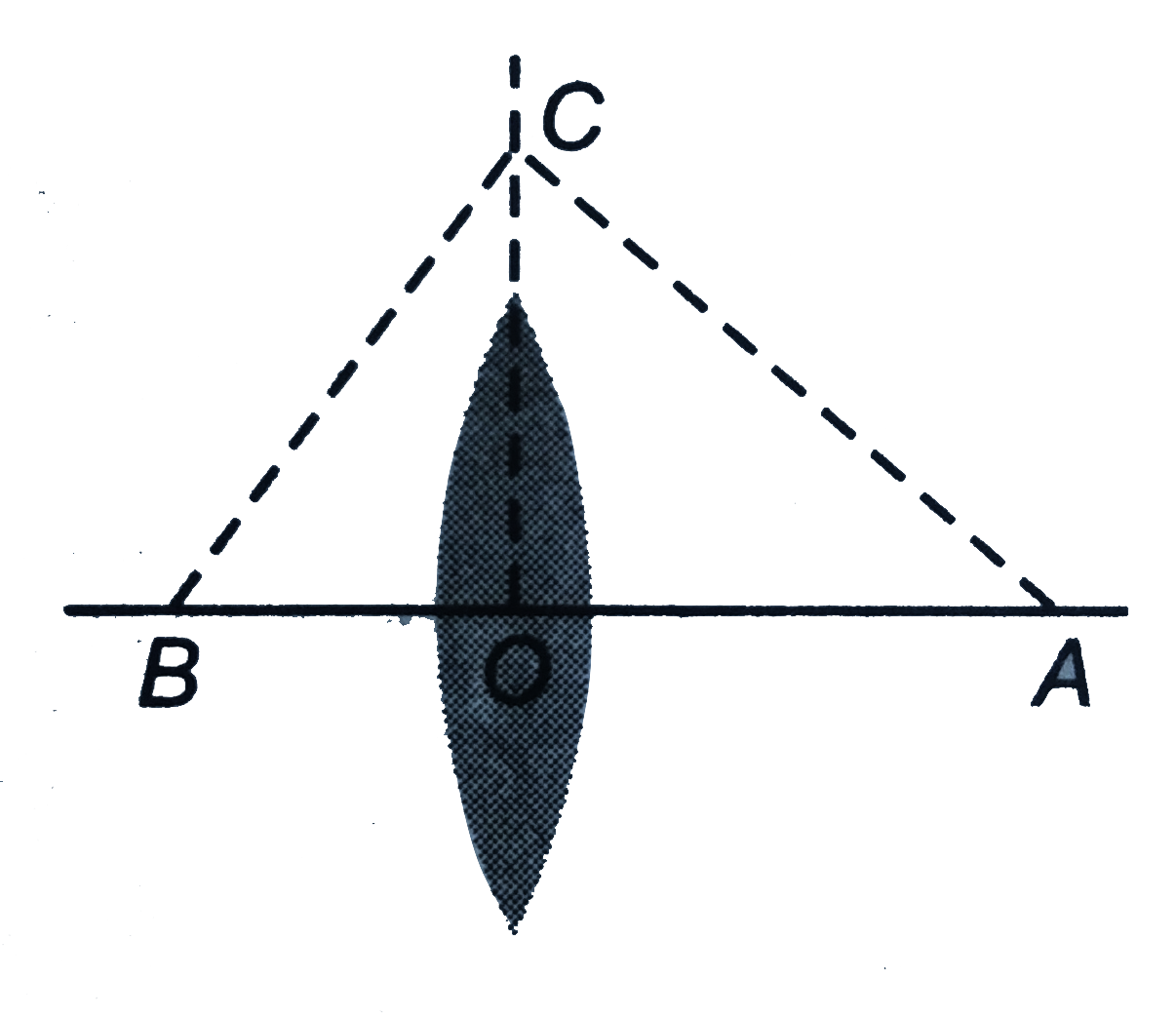
An object is placed at $A (O A > f)$ . Here, f is the focal length of the lens. The image is formed at B. A perpendicular is erected at O and C is chosen such that $∠ B C A = 90^{\circ}$ . Let OA = a, OB = b and OC = c. Then the value of f is

Video Solution

Text Solution

Verified by Experts

From $1 . v - \frac{1}{u} = \frac{1}{f}$ we have $\frac{1}{b} + \frac{1}{a} = \frac{1}{f}$
or $f = \frac{a b}{a + b} \to (1)$
further $A C^{2} + B C^{2} = A B^{2}$
or $(a^{2} + c^{2}) + (b^{2} + c^{2}) = {(a + b)}^{2}$
$a b = c^{2}$
Substituting this in Eq. (1) we get f= $\frac{c^{2}}{a + b}$

|

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If an object is placed at $A (O A > f),$ where f is the focal length of the lens, the image is formed at B. A perpendicular is erected at O and C is chosen on it such that the angle $(∠ B C A)$ is a right angle. Then, the value of f will be
A $\frac{A B}{O C^{2}}$
B $\frac{(A C) (B C)}{O C}$
C $\frac{O C^{2}}{A B}$
D $\frac{(O C) (A B)}{A C + B C}$
Question 2 - Select One
OABC is a parallelogram such that $O A = a, O B = b and O C = c$ , then the value $\to O A . \to B A$ is
A $\frac{a^{2} + 3 b^{2} + c^{2}}{2}$
B $\frac{a^{2} - b^{2} + 3 c^{2}}{2}$
C $\frac{a^{2} + 3 b^{2} - c^{2}}{2}$
D $\frac{3 a^{2} + b^{2} - c^{2}}{2}$
Question 3 - Select One
When an object is placed between O and $F_{1}$ in front of a convex lens, the image formed
Aenlarged and erect
Bdiminished and erect
Creal and enlarged
Ddiminished and inverted

NARAYNA-RAY OPTICS AND OPTICAL INSTRAUMENTS -EXERCISE- 4 One or more than one correct answer type

Home
Ask Doubt
Profile