The maximum potential that can be measured with a voltmeter of resistance 1000 Ω is 6V. Resistance that must be connected to measure a potential of 30V with it is
4000Ω in series
6000Ω in series
`12000 Omega` in series
2000Ω in series
The correct Answer is:A
To solve the problem, we need to determine the resistance that must be connected to a voltmeter in order to measure a potential of 30V, given that the voltmeter can measure a maximum potential of 6V with a resistance of 1000 ohms.
1. Understand the given values:
- Maximum potential (V1) = 6V
- Resistance of the voltmeter (R1) = 1000 ohms
- Desired potential (V2) = 30V
2. Use the relationship between the voltages and resistances:
The relationship can be expressed as:
V1V2=R1R1+R2
Here, R2 is the resistance that we need to find.
3. Substitute the known values into the equation:
630=10001000+R2
4. Cross-multiply to eliminate the fraction:
6(1000+R2)=30×1000
5. Expand and simplify the equation:
6000+6R2=30000
6R2=30000−6000
6R2=24000
6. Solve for R2:
R2=240006=4000 ohms
7. Conclusion:
The resistance that must be connected to measure a potential of 30V with the voltmeter is 4000 ohms.
- Maximum potential (V1) = 6V
- Resistance of the voltmeter (R1) = 1000 ohms
- Desired potential (V2) = 30V
The relationship can be expressed as:
V1V2=R1R1+R2
Here, R2 is the resistance that we need to find.
630=10001000+R2
6(1000+R2)=30×1000
6000+6R2=30000
6R2=30000−6000
6R2=24000
R2=240006=4000 ohms
The resistance that must be connected to measure a potential of 30V with the voltmeter is 4000 ohms.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 1(H.W) (AMPERE.S CIRCUITAL LAW BIOT-SAVART LAW AND ITS APPLICATIONS
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 1(H.W) (SOLENOID AND TOROID)
1 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 1(C.W) (MOVING COIL GALVANOMETER)
2 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
The maximum safe voltage that can be measured using a galvanometer of resistance G is Vm . Find the resistance to be connected in series with the galvanometer so that it becomes a voltmeter of range nVm.
View SolutionThe emf of a battery is 4.0 V and its internal resistance is 1.5Ω. Its potential difference is measured by a voltmeter of resistance 1000Ω. Calculate the percentage error in the reading of emf shown by voltmeter.
View Solution
Knowledge Check
The maximum potential that can be measured with a voltmeter of resistance 1000Ω is 6V. Resistance that must be connected to measure a potential of 30V with it is
A4000Ω in SeriesB6000Ω in SeriesC12000Ω in SeriesD2000Ω in SeriesThe range of voltmeter of resistance 300Ω is 5 V. The resistance to be connected to convert it into an ammeter of range 5 A is
A1Ωin seriesB1Ωin parallelC0.1Ωin seriesD0.1Ωin parallelThe range of voltmeter of resistance 300 Ω is 5 V. The resistance to be connected to convert it into an amineter of range 5 A is
A1Ω in seriesB1Ωin parallelC0.1Ω in seriesD0.1Ω in parallel
(a)find the potential drops across the two resistors shown in figure. (b) A voltmeter of resistance (600Ω)is used to measure the potential drop across the (300Ω) resistor.What will be the measured potential drop?
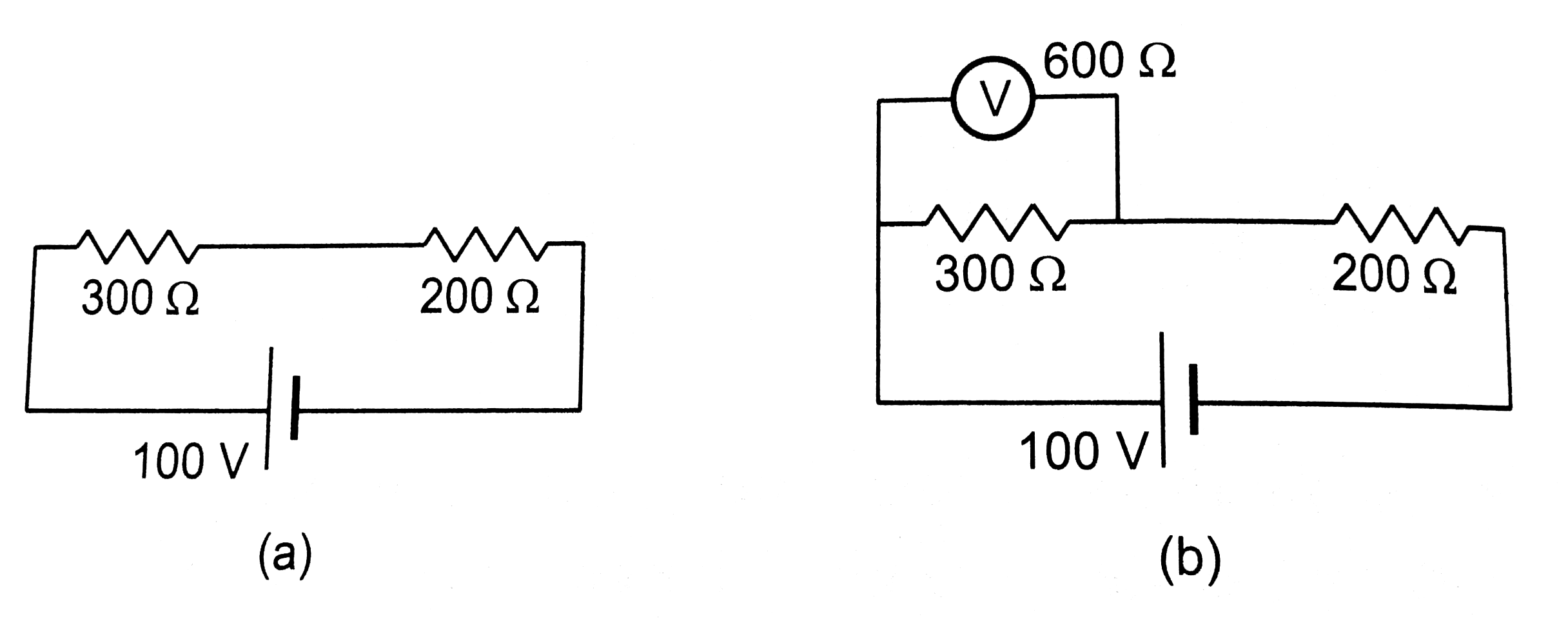
View SolutionThe maximum current that can be measured by a galvanometer of resistance 40Ω is 10 mA . It is converted into a voltmeter that can read upto 50 V . The resistance to be connected in series with the galvanometer is ... (in ohm )
View SolutionThe maximum current that can be measured by a galvanometer of resistance 40Ω is 10 mA . It is converted into a voltmeter that can read upto 50 V . The resistance to be connected in series with the galvanometer is ... (in ohm )
View SolutionA voltmeter has a resistance of 100Ω and measures 10 V. How can it be used to meaure 50 V ?
View SolutionA voltmeter can measure upto 25 volt and its resistance is 1000Ω. The resistance required to add with voltmeter to measure upto 250 volt will be-
View Solution
