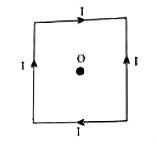
A wire in the form of a square of side '2m' carries a current 2A. Then the magentic induction at the centre of the square wire is ( magnetic permeability of free space =μ0)
μ02π
μ0√2π
2√2μ0π
μ0√2π
The correct Answer is:C
B=8√2μ0i4πa
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 1(C.W) (TANGENT GALVANOMETER)
4 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 1(C.W) (CURRENT LOOP AND MAGNETIC DIPOLE)
2 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - C.U.Q (CONVERSION OF MCG INTO VOLTMETER)
9 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
A wire of length l is bent in the form of a square and carries a current I. What is the value of its magnetic moment?
View SolutionA wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?
View Solution
Knowledge Check
A wire in the from of a square of side 'a' carries a current i. Then the magnetic induction at the centre of the square wire is (Magnetic permeability of free space=μ0)
Aμ0i2πaBμ0i√2πaC2√2μ0iπaDμ0i√2πaA square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0IπaA square wire of each side l carries a current I. What is the magnetic field at the midpoint of the square ?
 A4√2μo4πlIB8√2μo4πlIC16√2μo4πlID32√2μo4πlI
A4√2μo4πlIB8√2μo4πlIC16√2μo4πlID32√2μo4πlI
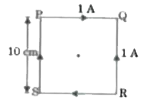
Calculate the magnetic field induction at the centre of a square shaped coil of side 10 cm, if it carries of current of 1A.
View SolutionTwo identical wires A and B have the same length L and carry the same current I. Wire A is bent into a circle of radius R and wire B is bent to form a square of side a. If B1andB2 are the values of magnetic induction at the centre of the square respectively, then the ratio is B1B2 is
View SolutionA wire in the from of a circular loop of one turn carrying a current produces a magnetic fild B at the centre. If the same wire is looped into a coil of two turns and carreis the same current, the new value of magnetic induction at the centre is
View SolutionA solenoid of length 50 cm and a radius of cros section 1 cm has 1000 turns of wire wound over it if the current carried is 5A the magnetic field on its axis near the centre of the solenoid is approximately (Given permeability of free space μ0=4π×10−7T−mA−1)
View SolutionTwo identical wires A and B have the same length l and carry the same current I. Wire A is bent into a circle of radius R and wire B is bent to form a square of side a. If B1andB2 are the values of magnetic induction at the centre of the circle and the centre of the square, respectively, then the ratio B1/B2 is
View Solution
