A flat insulating disc of radius $' a'$ carries an excess charge on its surface is of surface charge density $σ C / m^{2}$ . Consider disc to rotate around the perpendicular to its plane with angular speed $ω r a d / s$ / If magnetic field $\to B$ is directed perpendicular to the roation axis, then find the torque acting on the disc.

Video Solution

Text Solution

Verified by Experts

Suppose the disc is placed in xy-plane and is rotated about the z-axis. Consider an annular ring of radius rand of thickness dr, the charge on this ring.
$d q = σ (2 π d r)$
As the ring rotates with angular velocity $ω$ , so the current $i = \frac{d q}{d t} = \frac{σ (2 π r d r)}{\frac{2 π}{ω}} = σ ω r d r$

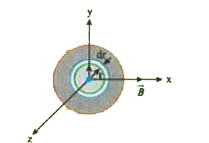
The torque on the current loop $\to τ = i \to A \times \to B$
Hence the torque on this annular ring $d \to τ = i (d \to A \times \to B) = σ ω r d r (π r^{2} B {sin 90}^{\circ})$
$= π σ ω r^{3} B d r and τ = π σ ω B \int^{a} r^{3} d r = \frac{π σ ω B a^{4}}{4}$

Updated on:21/07/2023

A long, hollow insulating cylinder of radius R and negligible thickness has a uniform surface charge density $σ$ . The cylinder rotates about its central axis at a constant angular speed $ω$ . Choose the correct option(s):
AThe charge crossing an imaginary line of length L on the surface of the cylinder, parallel to its axis, per unit time, is $ω σ R L$ .
BThe magnetic moment of a length L of the cylinder is $π ω σ R^{3} L$
CThe magnetic field intensity at a point on the axis of the cylinder, inside the cylinder, is $μ_{0} ω σ R^{2}$
DIf the direction of rotation of the cylinder is reversed, the magnetic field at a point on the axis of the cylinder will also reverse direction