The current in a conductor varies with time as ampers. The electric charge that passes from to sec is
50 C
100 C
25 C
75 C
The correct Answer is:B
Similar Questions
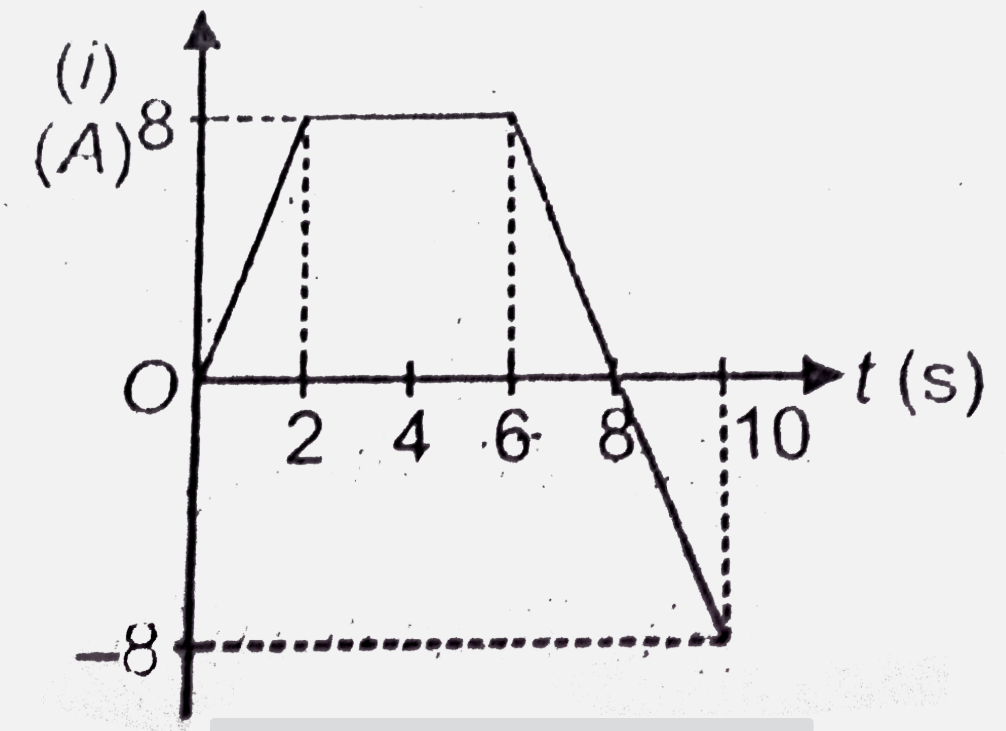
The current I through a conductor varies with time t as shown in figure. The average electric current during t=0 to t=10 s will be
View SolutionElectric current through a conductor varies with time as I(t)=50sin(100πt) .Hence I is in ampere and t in seconds.Total charge that passes any point from t=0 to t=1200S is
View Solution
Knowledge Check
The current in a conductor varies with time t as I=3t+4t2 Where I in amp and t in sec. The electric charge flows through the section of the conductor between t=1s and t=3s
A1003CB1274CC1403CD1503CThe current in conductor varies with time t as I=2t+3t2 where I is in ampere and t in seconds. Electric charge flowing through a section of the conductor during t=2sec to t=3sec is
A10CB24CC33CD44CThe current in a 90mH inductor changes with time as i=1.0t2, where I is in amperes and t is in seconds.
Athe magnitude of the induced emf at t=4.0s is 180 mVBthe emf zero at time t=3.0sCthe magnitude of the induced emf at t=4.0s is 360 mVDthe emf zero at time t=4.0s
Current passing through a conductor changes with time as i=10e−2t ampere. Charge passed through a cross-section of conductor in the time-interval t = 0 to t=∞ is______(in Coulomb).
View SolutionThe current through a wire connected to a condenser varies with time as i=(2t+1)A the charge transport to the condenser from t=0 to t=5s is
View SolutionThe current through a wire connected to a condenser varies with time as i=(2t+1)A the charge transport to the condenser from t=0 to t=5s is
View SolutionThe electric current in a circuit is given by
i=3t
Here, t is in second and I in ampere. The rms current for the period to=0 to t=1 s is
View SolutionElectric current in a wire is time rate of flow of charge. The charge in coulombs that passes through a wire after t seconds is given by the function q(t)=t2−2t2+5t+2. Determine the average current (in coulmbe per second) during the first two seconds.
View Solution
