The work done in deflecting a dipole through from field direction is
perpendicular to each other
2PE
zero
The correct Answer is:B
To find the work done in deflecting a dipole through 180∘ from the direction of the electric field, we can follow these steps:
Step 1: Understand the Dipole and Electric Field
A dipole consists of two equal and opposite charges, +Q and -Q, separated by a distance 2L. The dipole moment P is given by:
P=Q⋅2L
The dipole is placed in an electric field E.
Step 2: Determine the Torque on the Dipole
The torque τ acting on the dipole in an electric field is given by:
τ=PEsinθ
where θ is the angle between the dipole moment and the electric field direction.
Step 3: Work Done in Rotating the Dipole
The work done W in rotating the dipole from an angle θ1 to θ2 is given by the integral of torque over the angle:
W=∫θ2θ1τdθ
Substituting the expression for torque:
W=∫θ2θ1PEsinθdθ
Step 4: Integrate the Torque Expression
The integral of sinθ is −cosθ:
W=PE(−cosθ)θ2θ1=PE(−cosθ2+cosθ1)
Step 5: Substitute the Limits for the Integral
If we are rotating the dipole through 180∘, we can set θ1=0∘ (initially aligned with the electric field) and θ2=180∘:
W=PE(−cos180∘+cos0∘)
Knowing that cos180∘=−1 and cos0∘=1:
W=PE(−(−1)+1)=PE(1+1)=2PE
Step 6: Conclusion
Thus, the work done in deflecting the dipole through 180∘ from the direction of the electric field is:
W=2PE
A dipole consists of two equal and opposite charges, +Q and -Q, separated by a distance 2L. The dipole moment P is given by:
P=Q⋅2L
The dipole is placed in an electric field E.
The torque τ acting on the dipole in an electric field is given by:
τ=PEsinθ
where θ is the angle between the dipole moment and the electric field direction.
The work done W in rotating the dipole from an angle θ1 to θ2 is given by the integral of torque over the angle:
W=∫θ2θ1τdθ
Substituting the expression for torque:
W=∫θ2θ1PEsinθdθ
The integral of sinθ is −cosθ:
W=PE(−cosθ)θ2θ1=PE(−cosθ2+cosθ1)
If we are rotating the dipole through 180∘, we can set θ1=0∘ (initially aligned with the electric field) and θ2=180∘:
W=PE(−cos180∘+cos0∘)
Knowing that cos180∘=−1 and cos0∘=1:
W=PE(−(−1)+1)=PE(1+1)=2PE
Thus, the work done in deflecting the dipole through 180∘ from the direction of the electric field is:
W=2PE
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Exercise -1 (H.W)
Explore 43 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Exercise-2(C.W)
Explore 53 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:C.U.Q (Van De Graff Generator )
Explore 2 Videos
- ELECTROMAGNETIC WAVES Book:NARAYNAChapter:ELECTROMAGNETIC WAVES Exercise:EXERCISE -4
Explore 15 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Intergers type question
Explore 11 Videos
Similar Questions
An electric dipole consists of two opposite charges each of magnitude 1 mC separated by 2 cm. The dipole is placed in an external uniform field of 105NC−1 intensity. Find the
a. maximum torque exterted by the field on the dipole, and
b. work done in roating the dipole through 180∘ starting from the position θ=0∘.
View SolutionTwo point-charges +2eand−2e are situated at a distance of 2.4Å from each other and constitude an electric dipole. This dipole is placed in a uniform electric field of 4.0×105Vm−1. Calculate
(i) electric dipole moment,
(ii) potential energy of the dipole in equilibrium position,
(iii) work done in rotating the dipole through 180∘ from the equilibrium position.
View SolutionIn the figure shown, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole ?
(b) What is the work done in rotating the dipole through 180∘ ?
(c) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.
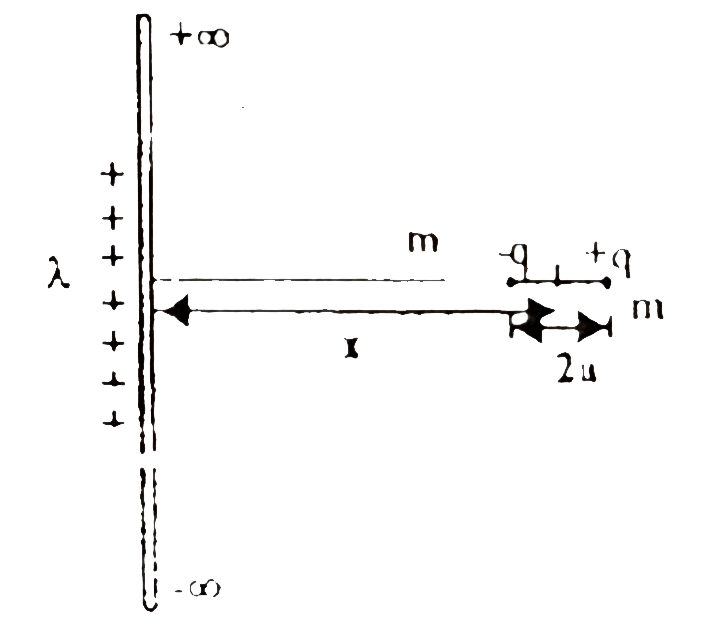
View SolutionIn figure-, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density λ.
(a) Find the net force acting on the dipole
(b) What is the work done in rotating the dipole through 180∘
(c ) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.
[(a)λaqπ∈0x2,(b)2λaqπ∈0x,(c)2π√2π∈0mx2aλq]

View SolutionWhat is the work done by a horse in displacing a cart through 15 m in the direction of the force , if the force applied by the horse is 10 N ?
View SolutionWhat is the work done by a horse in displacing a cart through 15 m in the direction of the force , if the force applied by the horse is 10 N ?
View SolutionWhat is the work done by a horse in displacing a cart through 5 m in the direction of the force if the force applied by the horse is 10 N?
View SolutionWhat is the work done by a horse in displacing a cart through 5 m in the direction of the force if the force applied by the horse is 10 N?
View SolutionA bar magnet of length 2 l and magnetic moment m is suspended freely in a uniform magnet field B. Find the amount of work done to deflect the magnet through an angle θ from the direction of the field.
View SolutionAn electric dipole of moment p is placed normal to the lines of force of electric field E, then the work done in deflecting it through an angle of 180 degree is
View Solution