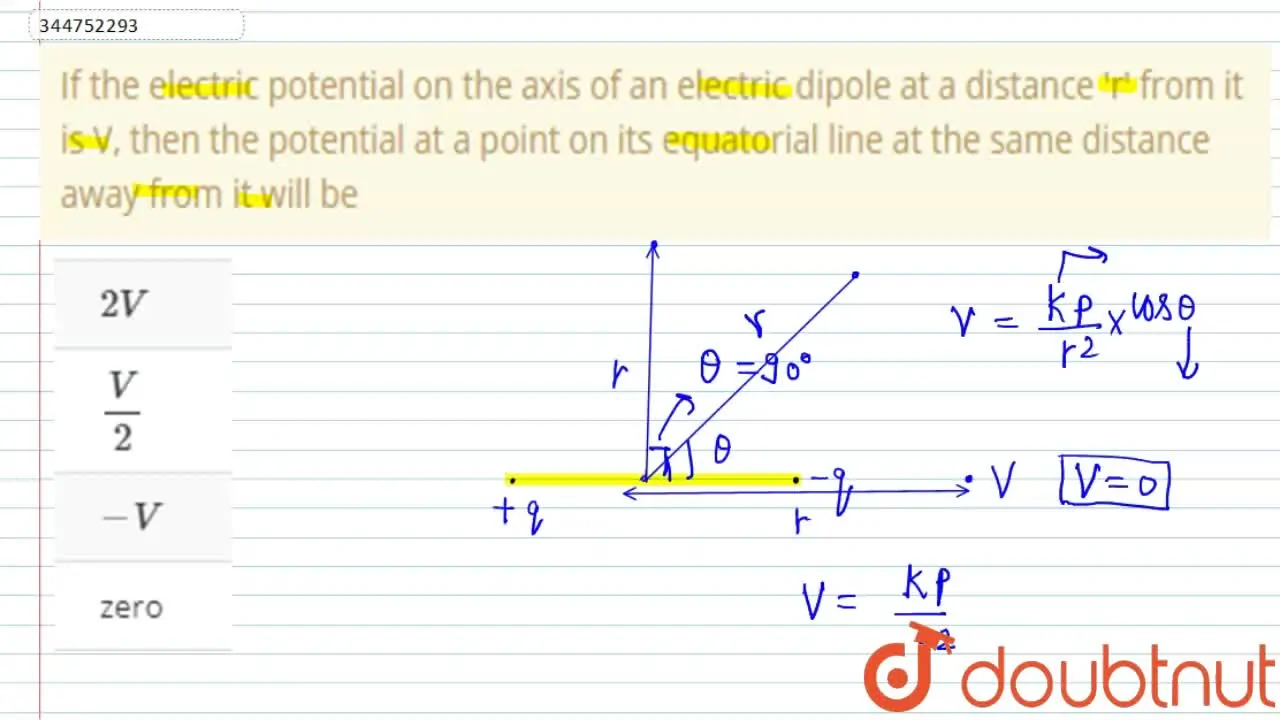
If the electric potential on the axis of an electric dipole at a distance 'r' from it is V, then the potential at a point on its equatorial line at the same distance away from it will be
2V
V2
−V
zero
The correct Answer is:D
Step by step video, text & image solution for If the electric potential on the axis of an electric dipole at a distance 'r' from it is V, then the potential at a point on its equatorial line at the same distance away from it will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-43videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-56videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluate yourself-28videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -415videos
ELECTROMAGNETIC WAVES
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question11videos
ELECTROSTATICS AND GAUSS LAW
Similar Questions
If the electric potential on the axis of an electric dipole at a distance 'r' from it is V, then the potential at a point on its equatorial line at the same distance away from it will be
View SolutionThe electric field and the potential of an electric dipole vary with distance 'r' as
View SolutionThe electric field and the potential of an electric dipole vary with distance r as
View SolutionThe electric potential due to an extermely short dipole at a distance r form it is proporitonal to
View SolutionThe electric potential at a point on the equatorial line of a electric dipole is
View SolutionThe electric potential at a point on the axis of an electric dipole depends on the distance r of the point from the dipole as
View SolutionThe electric potential V at a point on the axis of an electric dipole depends on the distance 'r of the point from the dipole as
View SolutionElectric potential (ϕ) of a quadrupole varies with distance 'r' on its axis as :-
View SolutionThe electric field due to a dipole at a distance r from its centre is proportional to
View SolutionElectric potential at any point in equatorial plane of a dipole is ………. .
View Solution