A ring with a uniform charge Q and radius R, is placed in the yz plane with its centre at the origin
The field at the origin is zero
The potential at the orgin is √kQR
The field at the point (x,0,0) is kQx2
The field at the point (x,0,0) is kQR2+x2
The correct Answer is:A
Field at the origin the centre of the ring is zero. Potential at the the orign =KQ/R.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -2 (H.W)
36 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -3
50 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -1 (H.W)
27 Videos
- DUAL NATUREBOOK - NARAYNACHAPTER - DUAL NATUREEXERCISE - LEVEL-II (H.W)
17 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level-II (H.W)
23 Videos
Similar Questions
The position of the centre of mass of a uniform semi-circular wire of radius 'R' placed in x-y plane with its centre at the origin and the line joining itsends as x-axis is given by (0,xRπ). Then the value of |x| is ______.
View SolutionA uniform semicircular ring of radius R is in yz plane with its centre at the origin. The half ring carries a uniform linear charge density of λ.
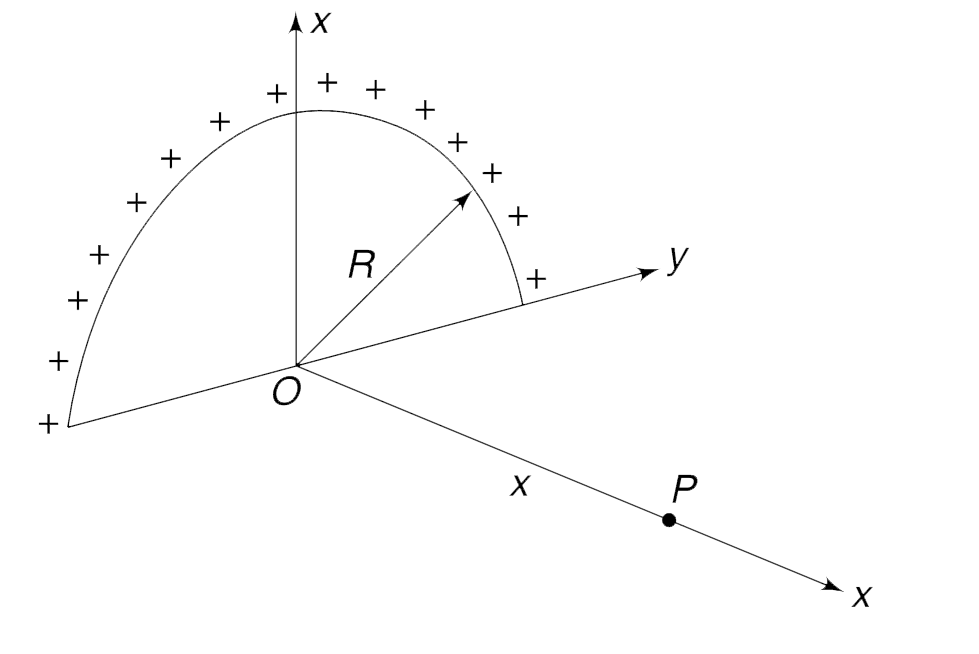
(a) Find the x, y and z component of Electric field at a point P(x, 0, 0) on the axis of the ring. (b) Prove that the field at P is directed along a line joining the centre of mass of the half ring to the point P.
View Solution
Knowledge Check
A point P(R√3,0,0) lies on the axis of ring of mass M and radius R the ring is located in YZ plane with its centre at origin O A small particle of mass m starts from P and reaches O under gravitatinal attracton only its speed at O will be
A√GMRB√GmRC√Gm2RD√Gm√2RA circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
Aλ3√3ε0RB2λ3√3ε0R2C23√3λε0RDnone the theseFor a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR
A circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View SolutionA thin wire carrying current i is bent to form a closed loop of one turn. The loop is placed in y-z plane with centre at origin. If R is the radius of the loop, then
View SolutionA ring of radius R is with a uniformly distributed charge Q on it .A charge q is now placed in the centre of the ring .Find the increment in tension in the ring.
View Solution. A small circular ring of radius R is placed in Y-Z plane with its centre at (−a,0,0). Another small circular ring of same radius Ris placed in X-Z plane with its centre at(0,−a,0). Calculate the magnitude and direction of net magnetic field at the origin (0, 0, 0), if both the rings carry current I. The direction of current in the first loop and the second loop is clockwise and anticlockwise respectively, when seen from the origin.
View SolutionA ring of radius R is placed in the plane with its centre at origin and its axis along the x−aξs and having uniformly distributed positive charge.A ring of radius r(<<R) and coaxial with the larger ring is moving along the axis with constant velocity then the variation of electrical flux (ϕ) passing through the smaller ring with position will be best represented by :
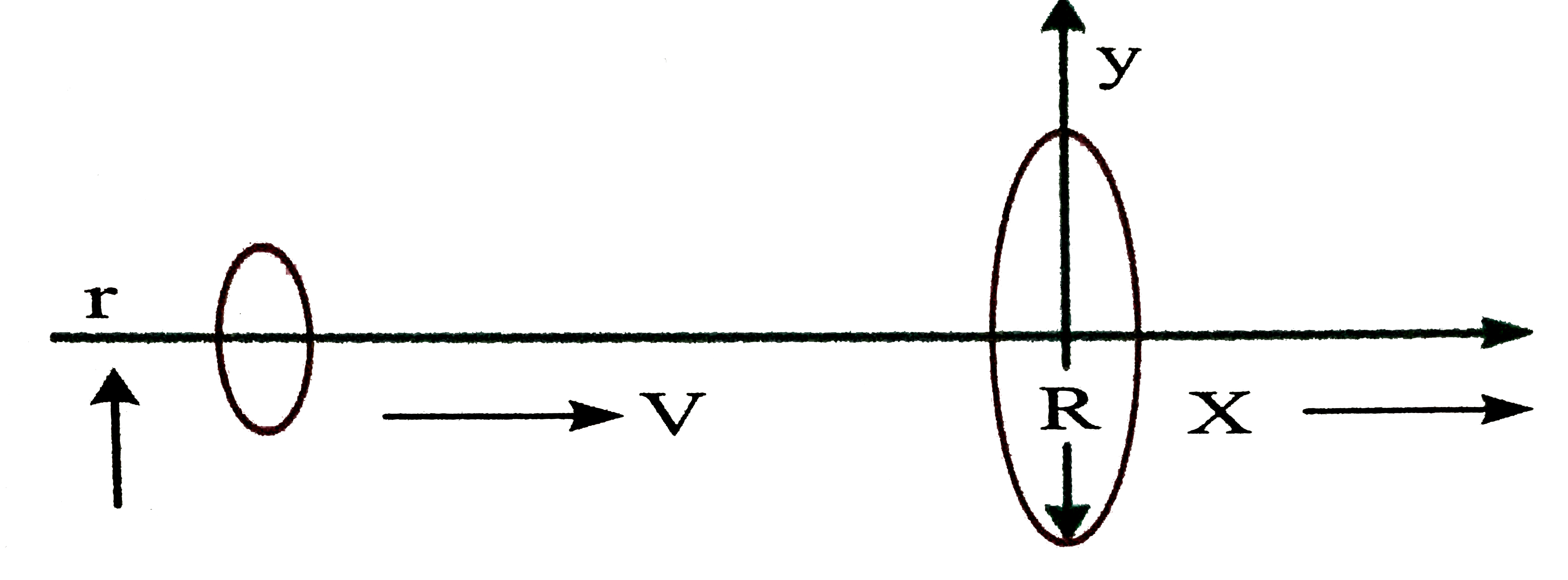
View Solution
