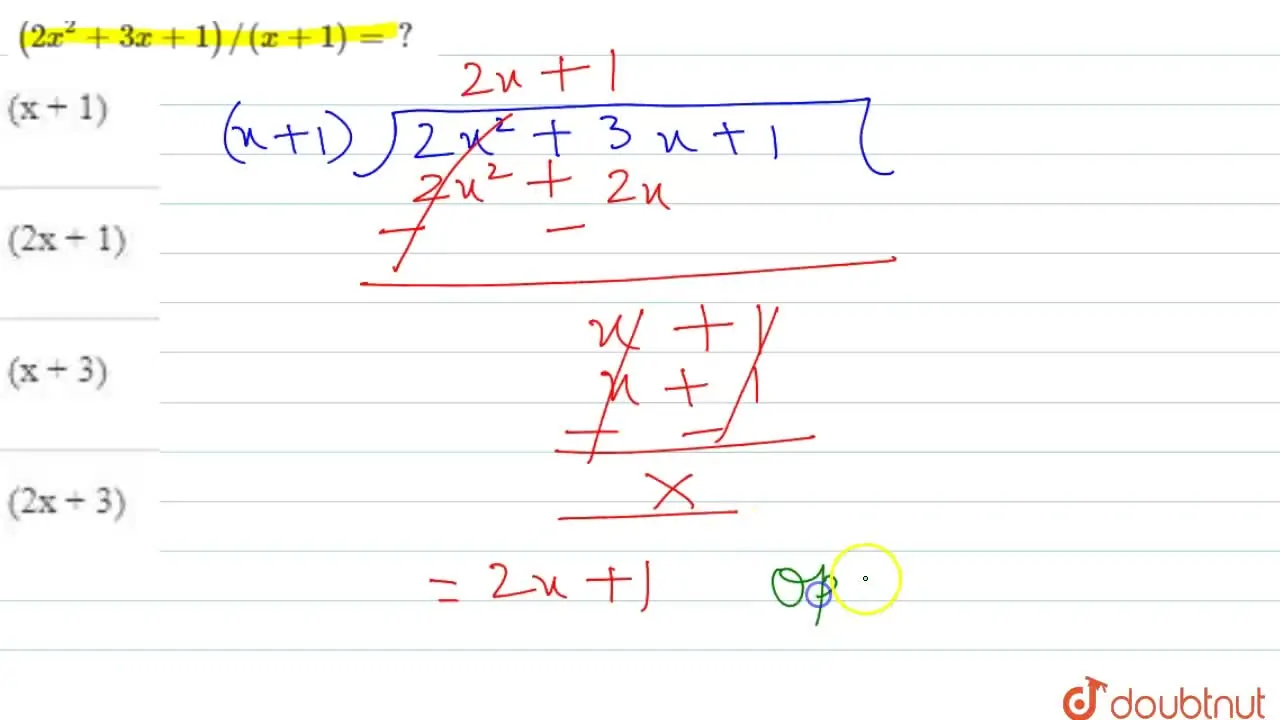(2x2+3x+1)/(x+1)=?
A
(x + 1)
B
(2x + 1)
C
(x + 3)
D
(2x + 3)
Video Solution
Text Solution
The correct Answer is:B
|
Answer
Step by step video, text & image solution for (2x^(2) + 3x + 1) // (x + 1) = ? by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - OPERATIONS ON ALGEBRAIC EXPRESSIONSEXERCISE - Exercise 6D15videos
OPERATIONS ON ALGEBRAIC EXPRESSIONS
- BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONSEXERCISE - TEST PAPER-8 (D) (Write .T. for true and .F. for false for each of the following:)1videos
LINEAR EQUATIONS
- BOOK - RS AGGARWALCHAPTER - PARALLELOGRAMSEXERCISE - Exercise 16B10videos
PARALLELOGRAMS
Similar Questions
limx→1[x3+2x2+x+1x2+2x+3]1−cos(x−1)(x−1)2
View SolutionSimplify the following
x−12x2+x−1−x+12x2−3x+1+42(x2−1)View SolutionFind the value of x for the following expression
x+12x2+x−1−x+12x2−3x+1+42(x2−1)=0View SolutionDivide 2x2+3x+1 by (x + 1)
View SolutionDivide 2x2+3x−1 by x + 1 and find the remainder.
View SolutionIf x2+3x+1x2−3x+1=12, then the value of x+1x is :
View Solution2x2−3x−459x2+1>1
View Solutionlimx→1x23−2x13+1(x−1)2
View SolutionThe non -integral roots of x4−3x3−2x2+3x+1=0 (1) are
View Solutionlimx→12(8x−32x−1−4x2+14x2−1)
View Solution