A 12.5 MeV α- particle approaching a gold nucleus is deflected 180∘ . What is the closest distance to which it approaches the nucleus ?
To solve the problem of finding the closest distance an alpha particle approaches a gold nucleus when it is deflected by 180 degrees, we can follow these steps:
1. Understanding the Problem:
- An alpha particle with a kinetic energy of 12.5 MeV is approaching a gold nucleus and is deflected by 180 degrees. We need to find the closest distance (R) it approaches the nucleus.
2. Convert Kinetic Energy to Joules:
- The kinetic energy (KE) of the alpha particle is given as 12.5 MeV.
- To convert MeV to Joules, we use the conversion factor:
1 MeV=1.6×10−13 Joules
- Thus,
KE=12.5 MeV×1.6×10−13 J/MeV=2.0×10−12 J
3. Use the Concept of Closest Approach:
- At the closest approach, the kinetic energy of the alpha particle is converted into potential energy (PE) due to electrostatic repulsion between the alpha particle and the gold nucleus.
- The potential energy is given by the formula:
PE=14πϵ0Q1Q2R
- Here, Q1 is the charge of the alpha particle and Q2 is the charge of the gold nucleus.
4. Calculate Charges:
- The charge of the alpha particle (Q1) is 2e (since it has 2 protons).
- The charge of the gold nucleus (Q2) is 79e (since gold has an atomic number of 79).
- Therefore,
Q1=2×1.6×10−19 C=3.2×10−19 C
Q2=79×1.6×10−19 C=1.264×10−17 C
5. Substituting Values into the Potential Energy Formula:
- The electrostatic constant 14πϵ0 is approximately 9×109 N m2/C2.
- Therefore, substituting the values into the potential energy equation:
PE=(3.2×10−19)(1.264×10−17)R
- Setting KE=PE:
2.0×10−12=(3.2×10−19)(1.264×10−17)R
6. Solving for R:
- Rearranging the equation gives:
R=(3.2×10−19)(1.264×10−17)2.0×10−12
- Calculating the numerator:
(3.2×10−19)(1.264×10−17)=4.0512×10−36
- Now, substituting this back:
R=4.0512×10−362.0×10−12=2.0256×10−24 m
7. Final Calculation:
- After calculating, we find:
R≈1.82×10−14 m
Final Answer:
The closest distance to which the alpha particle approaches the gold nucleus is approximately 1.82×10−14 m.
- An alpha particle with a kinetic energy of 12.5 MeV is approaching a gold nucleus and is deflected by 180 degrees. We need to find the closest distance (R) it approaches the nucleus.
- The kinetic energy (KE) of the alpha particle is given as 12.5 MeV.
- To convert MeV to Joules, we use the conversion factor:
1 MeV=1.6×10−13 Joules
- Thus,
KE=12.5 MeV×1.6×10−13 J/MeV=2.0×10−12 J
- At the closest approach, the kinetic energy of the alpha particle is converted into potential energy (PE) due to electrostatic repulsion between the alpha particle and the gold nucleus.
- The potential energy is given by the formula:
PE=14πϵ0Q1Q2R
- Here, Q1 is the charge of the alpha particle and Q2 is the charge of the gold nucleus.
- The charge of the alpha particle (Q1) is 2e (since it has 2 protons).
- The charge of the gold nucleus (Q2) is 79e (since gold has an atomic number of 79).
- Therefore,
Q1=2×1.6×10−19 C=3.2×10−19 C
Q2=79×1.6×10−19 C=1.264×10−17 C
- The electrostatic constant 14πϵ0 is approximately 9×109 N m2/C2.
- Therefore, substituting the values into the potential energy equation:
PE=(3.2×10−19)(1.264×10−17)R
- Setting KE=PE:
2.0×10−12=(3.2×10−19)(1.264×10−17)R
- Rearranging the equation gives:
R=(3.2×10−19)(1.264×10−17)2.0×10−12
- Calculating the numerator:
(3.2×10−19)(1.264×10−17)=4.0512×10−36
- Now, substituting this back:
R=4.0512×10−362.0×10−12=2.0256×10−24 m
- After calculating, we find:
R≈1.82×10−14 m
The closest distance to which the alpha particle approaches the gold nucleus is approximately 1.82×10−14 m.
Topper's Solved these Questions
- DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEIBook:CBSE COMPLEMENTARY MATERIALChapter:DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEIExercise:NUMERICALS
Explore 6 Videos
- CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)Book:CBSE COMPLEMENTARY MATERIALChapter:CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)Exercise:SECTION E
Explore 6 Videos
- ELECTROMAGNETIC WAVES AND OPTICSBook:CBSE COMPLEMENTARY MATERIALChapter:ELECTROMAGNETIC WAVES AND OPTICSExercise:1 mark question
Explore 11 Videos
Similar Questions
Knowledge Check
The distance oif closest approach of an alpha-particle fired towards a nucleus with momentum p is r. What will be the distance of closest approach when the momentum of alpha-particle is 2p?
A2rB4rCr/2Dr/4What is the distance of closest approach when a 5.0MeV proton approaches a gold nucleus?
A4×10−14mB2X10−14mC3×10−14mDNone of theseAn alpha particle of energy 5MeV is scattered through 180∘ by a found uramiam nucleus . The distance of closest approach is of the order of
A5.3×10−12mB5.3×10−13mC5.3×10−14mD5.3×10−15m
A 5MeVα particle is projected towards a stationary nucleus of atomic number 40. Calculate distance of closest approach.
View SolutionRutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α-scattering experiment. If an α-particle is projected from infinity with speed v towards the nucleus having Z protons, then the α-particle which is reflected back or which is deflected by 180∘ must have approached closest to the nucleus .It can be approximated that α particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then:
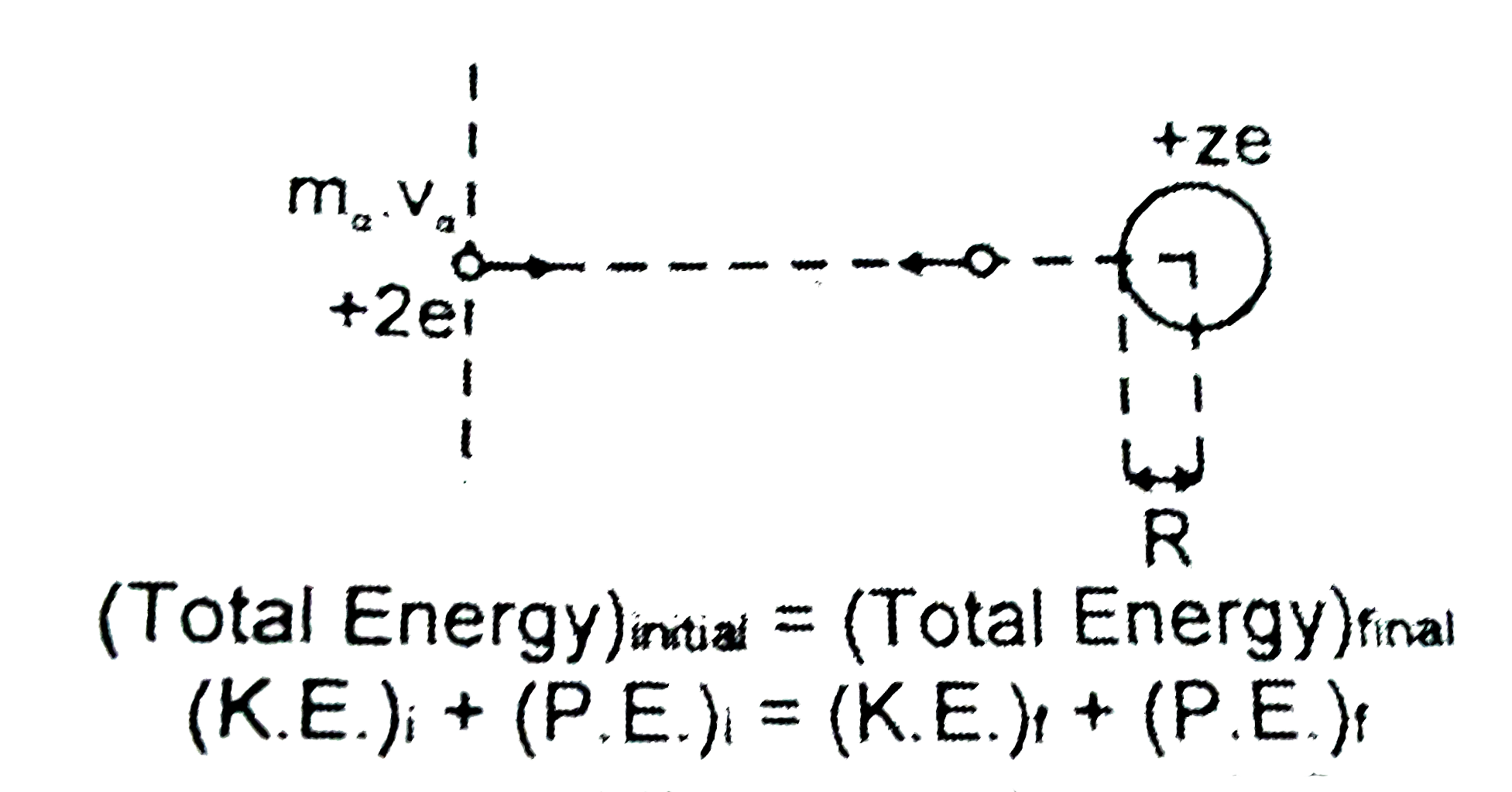
(P.E.)i=0, since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back.
12mαv2α+0=0+Kq1q2R⇒12mαv2α=K2e×ZeR⇒R=4KZe2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it
An α-particle with initial speed v0 is projected from infinity and it approaches up to r0 distance from a nuclie. Then, the initial speed of α-particle, which approaches upto 2r0 distance from the nucleus is :
View SolutionWhat is the distance of closest approach when a 5.0MeV proton approaches a gold nucleus?
View SolutionAn α-particle having K.E.=7.7MeV is scattered by gold (z=79) nucleus through 180∘ Find distance of closet approach.
View SolutionThe maximum K.E.found in alpha particle of natural origin is 7.7MeV .Find the closest distance of approach for the gold nucleus.
Z=79 for gold
[Note : At closest distance of approach, kinetic energy is converted into potential energy]
View Solution

