Sketch field lines due to (i) two equal positive charges near each other (ii) a dipole.
To sketch the electric field lines due to two equal positive charges near each other and a dipole, we can follow these steps:
Step 1: Sketching the Field Lines for Two Equal Positive Charges
1. Draw Two Positive Charges: Start by drawing two circles to represent the two equal positive charges. Label them as +q1 and +q2.
2. Indicate the Direction of Electric Field Lines: Since both charges are positive, the electric field lines will radiate outward from each charge.
3. Draw the Field Lines:
- From +q1, draw several lines radiating outward in all directions.
- From +q2, do the same, ensuring that the lines from both charges do not cross each other.
4. Show Repulsion: The lines between the two charges will bend away from each other due to the repulsive force between the two positive charges.
5. Finalize the Sketch: Ensure that the lines are evenly spaced and that they show the repulsion clearly.
Step 2: Sketching the Field Lines for a Dipole
1. Draw the Dipole: Represent the dipole by drawing a positive charge +q and a negative charge −q close to each other, with a small distance between them.
2. Indicate the Direction of Electric Field Lines: The electric field lines will originate from the positive charge and terminate at the negative charge.
3. Draw the Field Lines:
- From +q, draw lines radiating outward towards the negative charge.
- The lines should curve around the dipole, showing the attraction between the positive and negative charges.
4. Show the Field Lines' Behavior: Make sure to illustrate that the lines are denser near the charges and spread out as they move away from the dipole.
5. Finalize the Sketch: Ensure that the lines are drawn smoothly, indicating the direction of the electric field from the positive charge to the negative charge.
Final Sketches
- For the two equal positive charges, the field lines will show repulsion and will be bent away from each other.
- For the dipole, the field lines will show attraction, originating from the positive charge and terminating at the negative charge.
1. Draw Two Positive Charges: Start by drawing two circles to represent the two equal positive charges. Label them as +q1 and +q2.
2. Indicate the Direction of Electric Field Lines: Since both charges are positive, the electric field lines will radiate outward from each charge.
3. Draw the Field Lines:
- From +q1, draw several lines radiating outward in all directions.
- From +q2, do the same, ensuring that the lines from both charges do not cross each other.
4. Show Repulsion: The lines between the two charges will bend away from each other due to the repulsive force between the two positive charges.
5. Finalize the Sketch: Ensure that the lines are evenly spaced and that they show the repulsion clearly.
1. Draw the Dipole: Represent the dipole by drawing a positive charge +q and a negative charge −q close to each other, with a small distance between them.
2. Indicate the Direction of Electric Field Lines: The electric field lines will originate from the positive charge and terminate at the negative charge.
3. Draw the Field Lines:
- From +q, draw lines radiating outward towards the negative charge.
- The lines should curve around the dipole, showing the attraction between the positive and negative charges.
4. Show the Field Lines' Behavior: Make sure to illustrate that the lines are denser near the charges and spread out as they move away from the dipole.
5. Finalize the Sketch: Ensure that the lines are drawn smoothly, indicating the direction of the electric field from the positive charge to the negative charge.
- For the two equal positive charges, the field lines will show repulsion and will be bent away from each other.
- For the dipole, the field lines will show attraction, originating from the positive charge and terminating at the negative charge.
Topper's Solved these Questions
- ELECTROSTATICS AND CURRENT ELECTRICITY Book:CBSE COMPLEMENTARY MATERIALChapter:ELECTROSTATICS AND CURRENT ELECTRICITY Exercise:SHORT ANSWER QUESTIONS (2 MARKS)
Explore 59 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY Book:CBSE COMPLEMENTARY MATERIALChapter:ELECTROSTATICS AND CURRENT ELECTRICITY Exercise:SHORT ANSWER QUESTIONS (3 MARKS )
Explore 23 Videos
- ELECTRONIC DEVICES Book:CBSE COMPLEMENTARY MATERIALChapter:ELECTRONIC DEVICES Exercise:NUMERICALS
Explore 7 Videos
- SAMPLE QUESTION PAPER 2019Book:CBSE COMPLEMENTARY MATERIALChapter:SAMPLE QUESTION PAPER 2019Exercise:Section C
Explore 19 Videos
Similar Questions
Knowledge Check
Consider the following statements.
I The magnetic field lines of a magnet (or a solenoid) form continuous closed loops. This is unlike the electric dipole where these field lines begin from a positive charge and end on the negative charge or escape to infinity.
II The tangent to the field line at a given point represents the direction of the net magnetic field B at that point.
III. The larger the number of field lines crossing per unit area, the stronger the magnitude of the magnetic field B.
IV. The magnetic field lines intersect each other. Which of the following statements are correct?AI, II and IVBI, III and IVCII, III and IVDI, II and IIIWhich of the following figure represents the electronic field lines due to a combination of the one positive and one negative charge?
A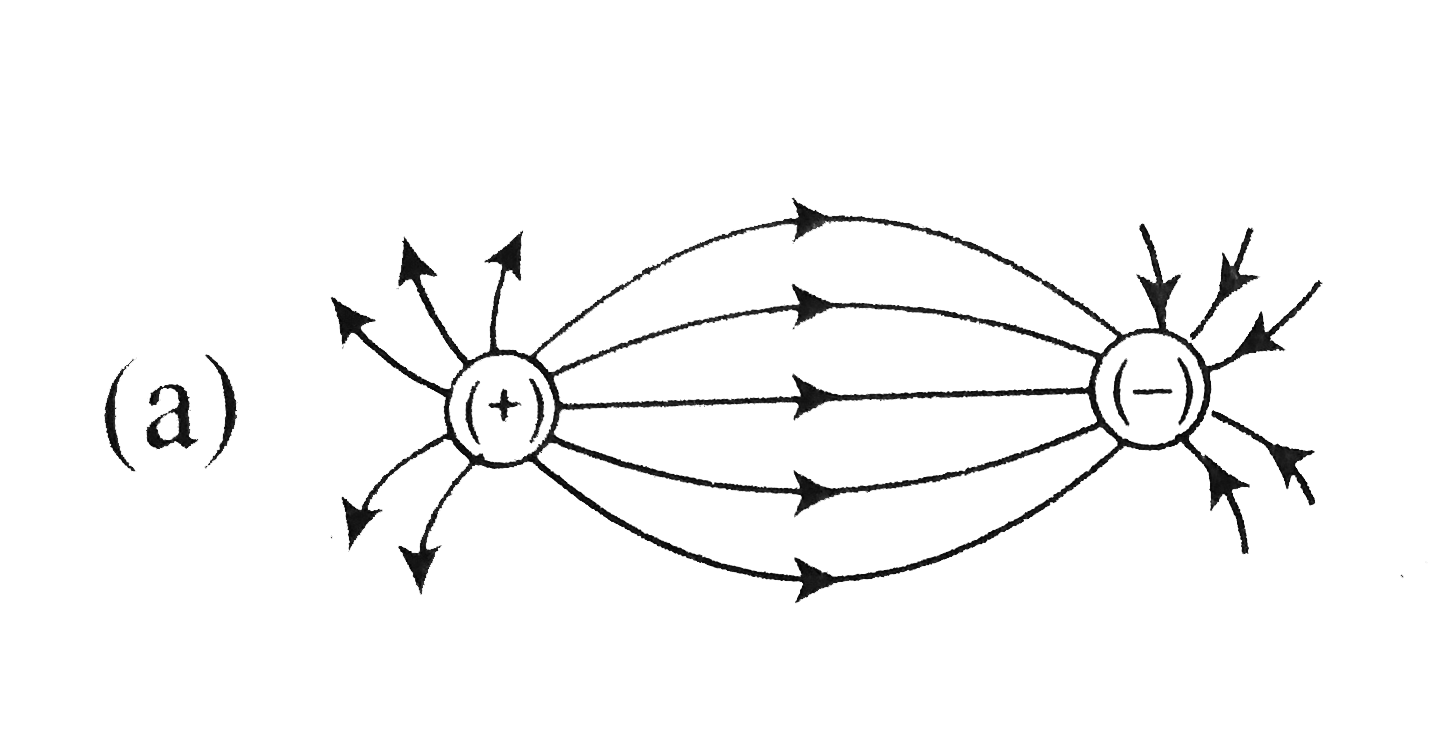 B
B C
C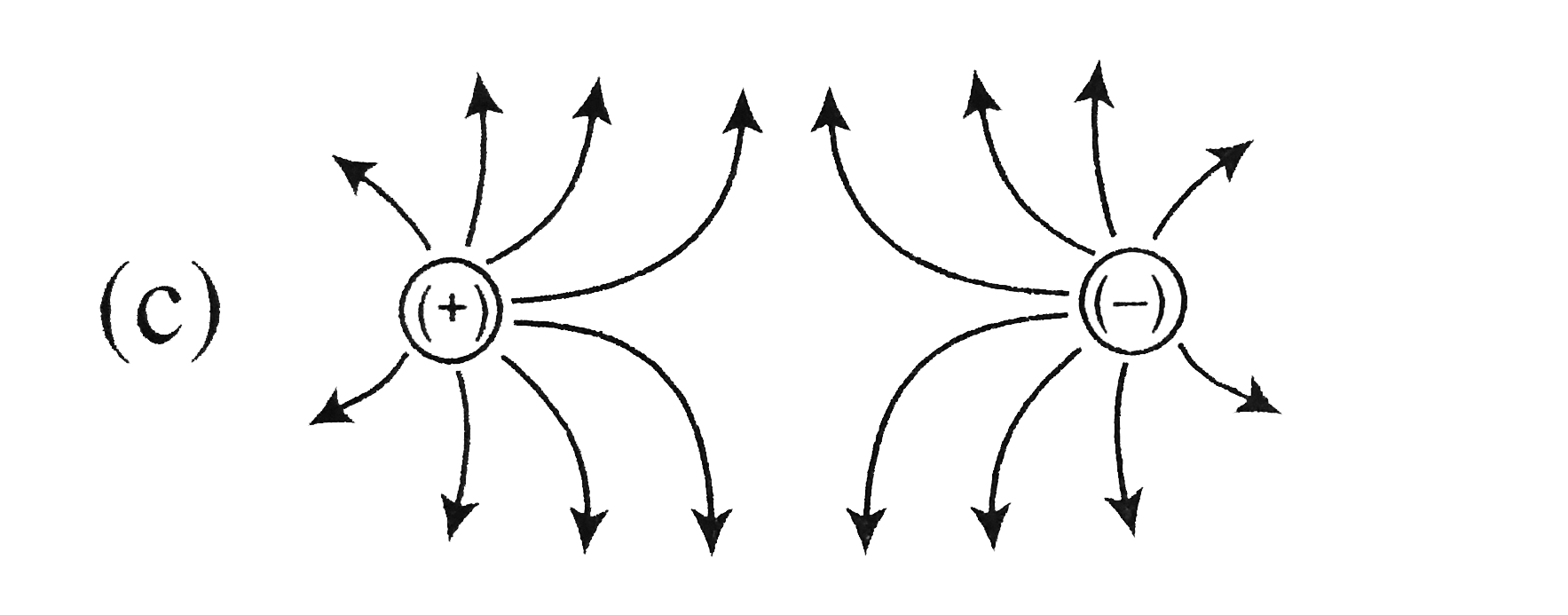 D
D
Draw the electric field lines due to two equal and opposite point charges.
View SolutionAn electric dipole is kept fixed at a location. A positive point charge is brought near the dipole. What will be the maximum number of null points by placing point charge at appropriate location with respect to electric dipole?
View SolutionWhat is an equipotential surface ? Write three properties Sketch equipotential surfaces of
(i) Isolated point charge
(ii) Uniform electric field
(iii) Dipole
View SolutionWhat are electric field lines? Why do two field lines never intersect each other?
View SolutionGive two properties of electric lines of force. Sketch them for an isolated positive point charge and an electric dipole.
View SolutionTwo equal and opposite charges of magnitude 10 μC each are fixed at a distance of 1 mm from each other to form an electric dipole . Calculate the electric field intensity (i) at a point on its axis at a distance 1 m from the centre of dipole and (ii)at a point on its perpendicular bisector at a distance 1 m from the centre of dipole.
View Solution

