If the point charge is now moved to a distance 'd' form the centre of the square and the side of the square is doubled explain how the electric flux will be affected.
To solve the problem, we need to analyze how the electric flux changes when a point charge is moved and the side length of the square is doubled. We will use Gauss's Law, which states that the electric flux (Φ) through a closed surface is proportional to the charge (Q) enclosed by that surface, given by the formula:
Φ=Qϵ0
where ϵ0 is the permittivity of free space.
1. Initial Setup:
- Consider a square with side length d that originally has a point charge Q at its center. The electric flux through the square can be calculated using Gauss's Law.
2. Calculate Initial Electric Flux:
- Since the charge Q is at the center of the square, the electric flux through the square is:
Φ1=Qϵ0
3. Move the Charge:
- Now, the charge is moved to a distance d from the center of the square. At this point, the charge is no longer at the center, but it is still within the bounds of the square.
4. Effect of Moving the Charge:
- The electric flux through the square does not depend on the position of the charge as long as the charge remains inside the Gaussian surface (the square). Therefore, the electric flux remains:
Φ2=Qϵ0
5. Doubling the Side Length of the Square:
- Next, the side length of the square is doubled, making it 2d. The new square now encloses the same charge Q.
6. Calculate New Electric Flux:
- Since the charge Q is still enclosed within the new square, the electric flux through this larger square is:
Φ3=Qϵ0
7. Conclusion:
- The electric flux through both the original square and the new larger square remains the same:
Φ1=Φ2=Φ3=Qϵ0
- Thus, the electric flux is unaffected by the movement of the charge or the change in the size of the square as long as the charge remains enclosed.
Summary:
The electric flux through the square remains constant regardless of the position of the charge (as long as it remains inside the square) and the size of the square, as it only depends on the amount of charge enclosed.
- Consider a square with side length d that originally has a point charge Q at its center. The electric flux through the square can be calculated using Gauss's Law.
- Since the charge Q is at the center of the square, the electric flux through the square is:
Φ1=Qϵ0
- Now, the charge is moved to a distance d from the center of the square. At this point, the charge is no longer at the center, but it is still within the bounds of the square.
- The electric flux through the square does not depend on the position of the charge as long as the charge remains inside the Gaussian surface (the square). Therefore, the electric flux remains:
Φ2=Qϵ0
- Next, the side length of the square is doubled, making it 2d. The new square now encloses the same charge Q.
- Since the charge Q is still enclosed within the new square, the electric flux through this larger square is:
Φ3=Qϵ0
- The electric flux through both the original square and the new larger square remains the same:
Φ1=Φ2=Φ3=Qϵ0
- Thus, the electric flux is unaffected by the movement of the charge or the change in the size of the square as long as the charge remains enclosed.
The electric flux through the square remains constant regardless of the position of the charge (as long as it remains inside the square) and the size of the square, as it only depends on the amount of charge enclosed.
Topper's Solved these Questions
Similar Questions
(a) Define electric flux. Is is the scalar or a vector quantity?
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown in the figure. Use Gauss's law to obtain the expression for the electric flux through the square.
(b) If the point charges is now moved to a distance 'd' from the centre of the square and the side of the square is doubled, explain how the electric flux will be affected.

View SolutionDefine electric flux, Is it a scalar or a vector quantity? A point charg q is at a distance of d2 directly above the centre of a square of side 'd' Use Gauss' law to obtain the expression for the electric flux through the square.
(b) If the point charge is now moved to a distance 'd' from the centre of the square and the side of the square is doubled , explain how the electric flux will be affected.
View Solution
Knowledge Check
If side of a square is doubled, how many times its area will be increased?
A5 timesB2 timesC4 timesD3 timesA point charge q is placed at a distance a/2 directly above the center of a square of side a. The electric flux through the square is
Aqε0Bqπε0Cq4ε0Dq6ε0
The side of a square is 5cm. How many times does the area increase, if the side of the square is doubled?
View SolutionA point charge Q is placed at the corner of a square of side a, then find the flux through the square.

View SolutionTwo point charges +Q each are placed at adjacent corners of a square. Other two point charges -Q each are placed at the remaining two corners of the same square . The side of the square is l. Find electric field intensity at the centre of the square.
View Solution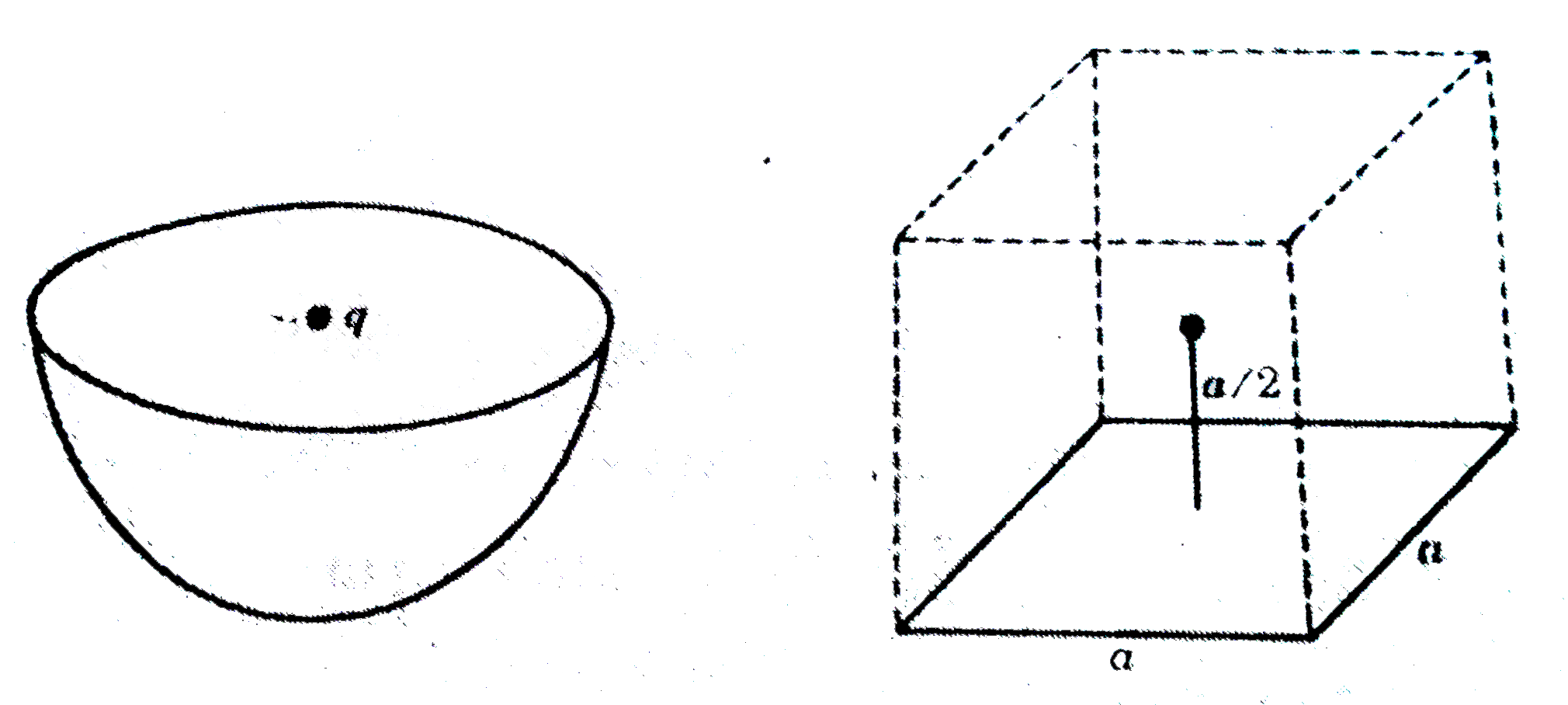
A point charge q is placed at a distnace a/2 directly above the centre of a square of side a, as shown figure. Find the magnitude of the electric flux through the square.
View SolutionA point charge Q is placed at the corner of a square of side a. Find the flux through the square.
View SolutionA point charge q is located at a very small distance form the center of a very large square on the line perpendicular to the square passing through its center Determine the approximate electric flux through the square due to the point charge.
View Solution
