Let f(x)=x2−11x+18x2−7x+12
Match List-I with List-II and select the correct answer using the code given below the list.
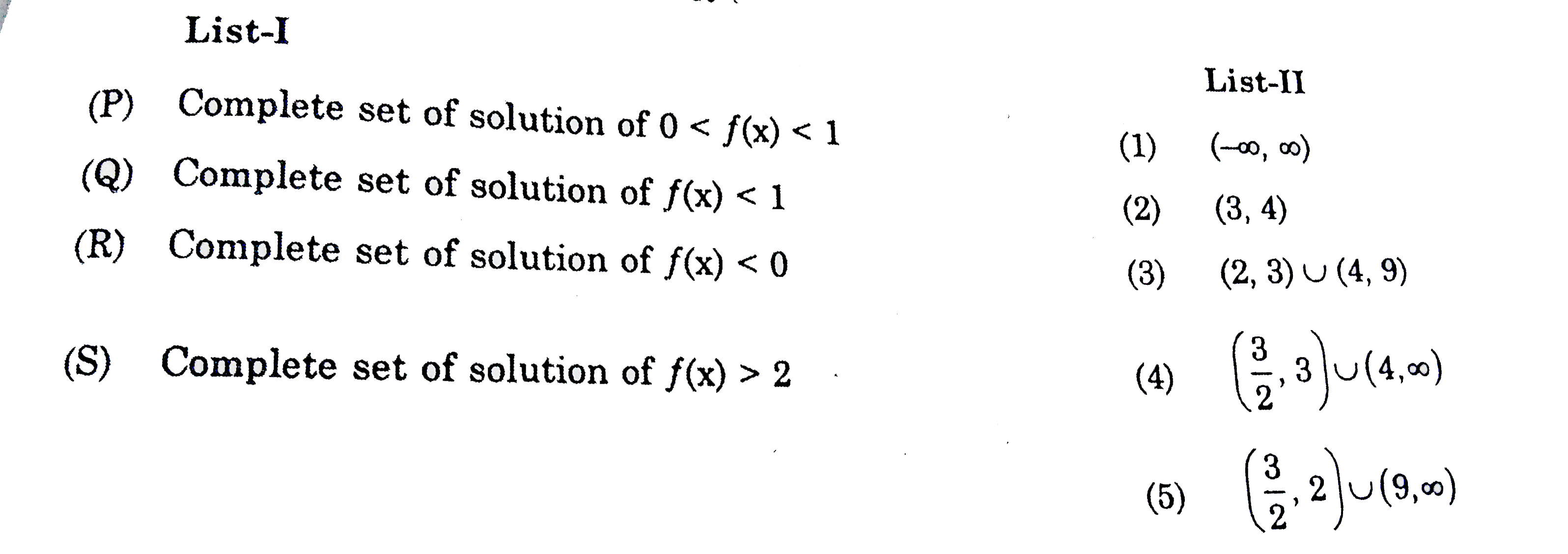
P→5 , Q→1 , R→3 , S→ 4
P→5 , Q→4 , R→3 , S→ 2
P→2 , Q→4 , R→3 , S→ 5
P→4 , Q→5 , R→3 , S→ 2
The correct Answer is:B
Step by step video, text & image solution for Let f(x)=(x^2-11x+18)/(x^2-7x+12) Match List-I with List-II and select the correct answer using the code given below the list. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:MATHEMATICS
Explore 20 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS SECTION-I
Explore 10 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:Chemistry
Explore 18 Videos
- SEQUENCE AND PROGRESSIONBook:ALLENChapter:SEQUENCE AND PROGRESSIONExercise:Exercise (JA)
Explore 12 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:CHEMISTRY
Explore 1 Video
Similar Questions
Match List-I with List-II and select the correct answer using the code given below the Lists :

View SolutionMatch List-I with List-II and select the correct answer using the code given below the Lists :

View SolutionMatch List-I with List-II and select the correct answer using the code given below the Lists :

View SolutionMatch List-I with List-II and select the correct answer using the code given below the Lists :

View SolutionMatch List-I with List-II and select the correct answer using the code given below the Lists:

View SolutionMatch List-I with List-II and select the correct answer using the code given below the Lists:

View SolutionMatch List-I with List-II and select the correct answer using the code given below the Lists :

View SolutionMatch List-I with List-II and select the correct answer using the code given below the Lists :

View SolutionMatch List-I with List-II and select the correct answer using the code given below the Lists :

View SolutionMatch List-I with List-II and select the correct answer using the code given below the Lists :

View Solution

