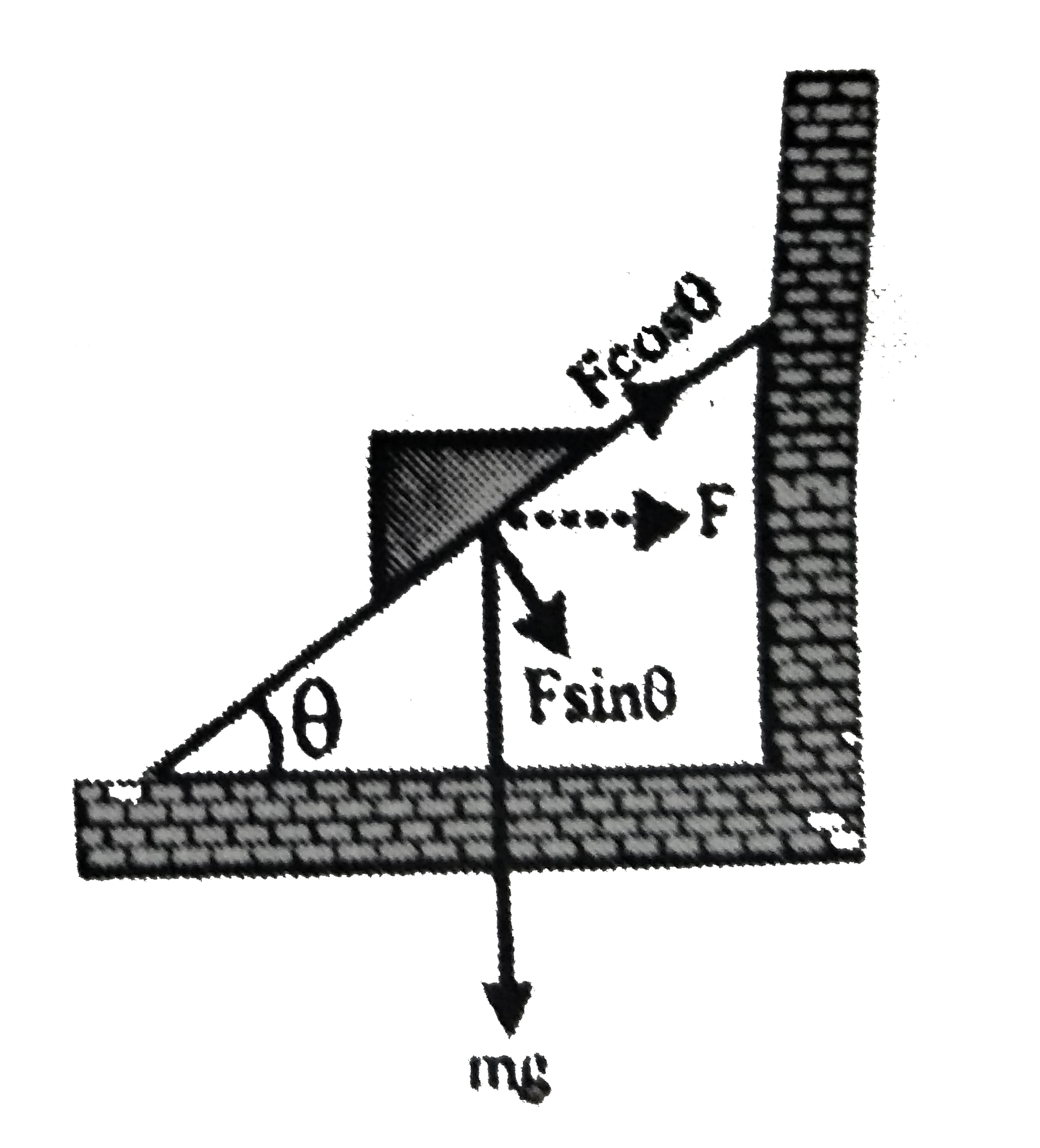
A block rests on a rough inclined plane as shown in Fig. 7.93 . A horizontal force is applied to it . (a) Find out the force of reaction .
(b) Can the force of friction be zero ? If yes , when ? (c) Assuming that , friction is not zero , find it magnitude and the direction of its limiting value .

(a) N=mgcosθ+Fsinθ
(b) Yes, if mg sinθ=Fcosθ
(c ) f=μR=μ(mgcosθ+Fsinθ), up the plane if the body has tendency to side down and down the plane if the body has tendency to move up.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-1)
26 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-2)
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
Similar Questions
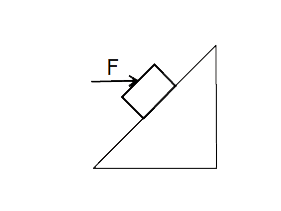
A block rest on a rough inclined plane as shown in fig. A horizontal force F is applied to it (a) Find out the force of reaction, (b) Can the force of friction be zero if yes when? And (c) Assuming that fricition is not zero find its magnitude and direction of its limiting value.

View SolutionA block is placed on a smooth inclined plane as shown . For what value of horizontal force F, the block will remain at rest ?

View Solution
Knowledge Check
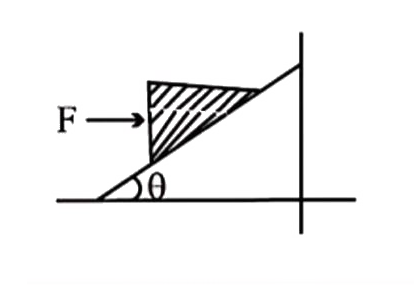
A block rests on a rough inclined plane as shown in figure. A horizontal force F is applied to it-
(a) Reaction on the block is Fsinθ+mgcosθ
(b) Frictional force is zero when Fcosθ=mgsinθ
(c) The value of limiting friction in μ(mgsinθ+Fcosθ)
(d)The value of limiting friction is μ(mgsinθ−Fcosθ)Aa, bBc, dCb, dDb, cA block rests on a fixed rough inclined place and a horizontal force F is applied to it, as shown in the figure. Which of the following statements are correct?
(A) Normal reaction on the block is Fsinθ+mgcosθ
(B) The friction force is zero when Fcosθ=mgsinθ
(C) The value of limiting friction is μ(mgsinθ+Fcosθ)
(D) The value of limiting friction is μ(mgsinθ−Fcosθ)
 A1,2B3,4C2,4D2,3
A1,2B3,4C2,4D2,3A block of mass 3kg is at rest on a rough inclined plane as shown in the figure. The magnitude of net force exerted by the surface on the block will be
 A26NB19.5NC10ND30N
A26NB19.5NC10ND30N
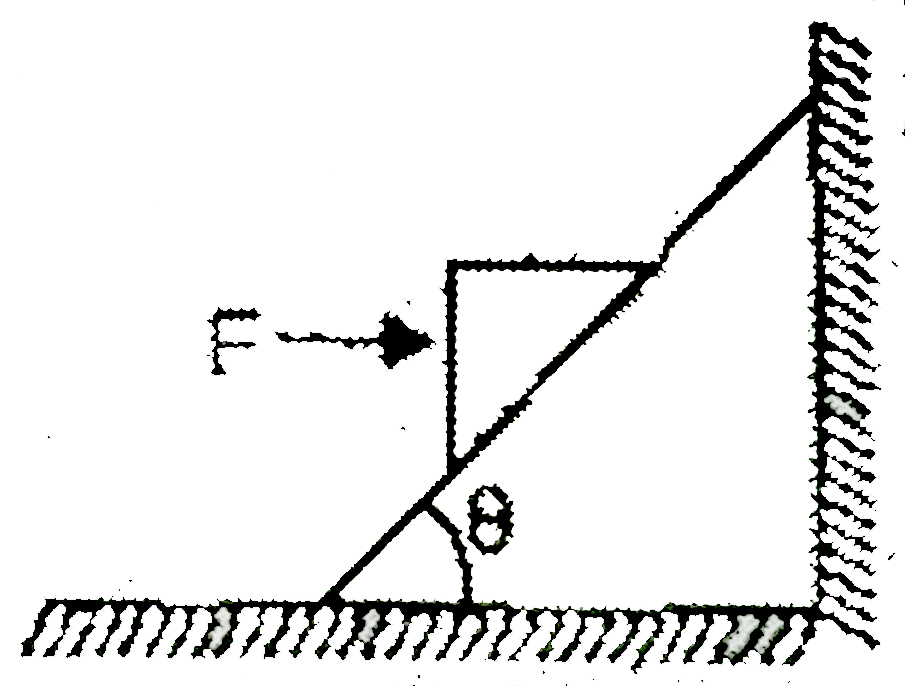
A triangular block mass m rests on a fixed rough inclined plane having friction coefficient μ with the block. A horizontal force F is applied to it as shown in figure below, then the correct statement is :
View SolutionA block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA triangular block of mass m rests on a fixed rough inclined plane having friction coefficient μ with the block. A horizontal forces F is applied to it as shown in figure below, then the correct statements is:

View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View Solution
