A force of 50 N acts in the direction as shown in figure. The block of mass 5kg. Resting on a smooth horizonatal surface. Find out the acceleration of the block.
To solve the problem step by step, we will follow these instructions:
Step 1: Identify the Given Values
- Force (F) = 50 N
- Mass (m) = 5 kg
- The angle of the force with the horizontal is not specified in the question, but we will assume it is at an angle θ (for example, 60 degrees as mentioned in the transcript).
Step 2: Resolve the Force into Components
Since the force is applied at an angle, we need to resolve it into its horizontal (x) and vertical (y) components:
- Horizontal component (F_x) = F * cos(θ)
- Vertical component (F_y) = F * sin(θ)
For our example with θ = 60 degrees:
- F_x = 50 * cos(60°) = 50 * (1/2) = 25 N
- F_y = 50 * sin(60°) = 50 * (√3/2) = 25√3 N
Step 3: Analyze the Forces Acting on the Block
Since the block is on a smooth horizontal surface, the only horizontal force acting on it is the horizontal component of the applied force (F_x). The vertical forces (normal force and weight) balance each other out.
Step 4: Apply Newton's Second Law
According to Newton's second law:
Fnet=m⋅a
Where:
- Fnet is the net force acting on the block.
- m is the mass of the block.
- a is the acceleration of the block.
In this case, the net force acting on the block in the horizontal direction is:
Fnet=Fx=25N
Step 5: Calculate the Acceleration
Now we can use the equation from Newton's second law to find the acceleration (a):
Fnet=m⋅a
Substituting the values we have:
25=5⋅a
Now, solve for a:
a=255=5m/s2
Final Answer
The acceleration of the block is 5m/s2.
---
- Force (F) = 50 N
- Mass (m) = 5 kg
- The angle of the force with the horizontal is not specified in the question, but we will assume it is at an angle θ (for example, 60 degrees as mentioned in the transcript).
Since the force is applied at an angle, we need to resolve it into its horizontal (x) and vertical (y) components:
- Horizontal component (F_x) = F * cos(θ)
- Vertical component (F_y) = F * sin(θ)
- F_x = 50 * cos(60°) = 50 * (1/2) = 25 N
- F_y = 50 * sin(60°) = 50 * (√3/2) = 25√3 N
Since the block is on a smooth horizontal surface, the only horizontal force acting on it is the horizontal component of the applied force (F_x). The vertical forces (normal force and weight) balance each other out.
According to Newton's second law:
Fnet=m⋅a
Where:
- Fnet is the net force acting on the block.
- m is the mass of the block.
- a is the acceleration of the block.
Fnet=Fx=25N
Now we can use the equation from Newton's second law to find the acceleration (a):
Fnet=m⋅a
Substituting the values we have:
25=5⋅a
a=255=5m/s2
The acceleration of the block is 5m/s2.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (S-1)
Explore 26 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (S-2)
Explore 9 Videos
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:SOLVED EXAMPLE
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
Similar Questions
A force of 100 N acts in the direction as shown in figure on a block of mass 10 kg resting on a smooth horizontal table. The speed acquired by the block after it has .moved a distance of 10 m, will be - (in m/sec) (g=10m/sec2)

View SolutionIn the figure shown, find out acceleration of each block.
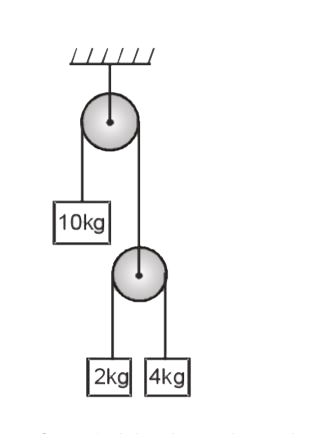
View Solution
Knowledge Check
A force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
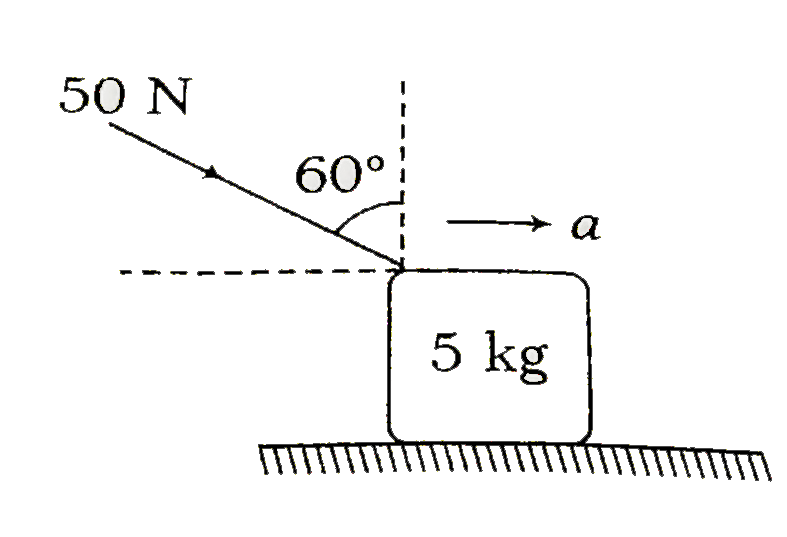 A5√3ms−2B2√3ms−2C15√3ms−2D3√3ms−2
A5√3ms−2B2√3ms−2C15√3ms−2D3√3ms−2Two forces act on a 4.5 kg block resting on a frictionless surface as shown in the given figure. What is the magnitude of the horizontal acceleration of the block ?
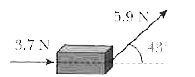 A1.8 m/s2B1.2 m/s2C0.82 m/s2D3.2 m/s2
A1.8 m/s2B1.2 m/s2C0.82 m/s2D3.2 m/s2A horizontal force ''F'' produces an acceleration of 6m/s−2 on a block resting on a smooth horizontal surface. The same force produces an acceleration of 3m/s−2 on a second block resting on a smooth horizontal surface. If the two blocks are tied together and the same force acts, the acceleration produced will be
A9m/s−2B2m/s−2C4m/s−2D12m/s−2
A rope of mass 0.5kg is pulling a block of mass 10kg under the action of force of 31.5N If the block is resting on a smooth horizontal surface calculate the force of reaction exerted by the block on the rope .
View SolutionTwo blocks of masses 4kg and 6kg are kept on a rough horizontal surface as shown. If the acceleration of 6kg block is 5n, then n is :

View SolutionA block of 10 kg mass is placed on a rough inclined surface as shown in figure. The acceleration of the block will be
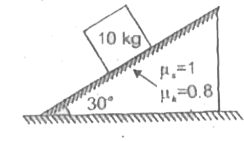
View SolutionA force of 9 N pulls a block of 4 kg through a rope of mass 0.5 kg. The block is resting on a smooth surface. What is the force of reaction exerted by the block on the rope?
View SolutionA block of mass m is kept over another block of mass 2m and the system rests on a smooth horizontal surface. The coefficient of friction between the block is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement the of the system when a force mg is applied to the lower block
View Solution

