Cement, sand and seree are dropped in rotating cylidrical drum to make concrete mixture. If rotating speed of drum is very high then contents are attached to wall of drum and mixture is not formed correctly. If radius of drum is 1.25 m and its axis is horizontal, then the required maximum rotating speed to make good mixture in rpm is -
8
0.4
1.3
27
The correct Answer is:D
Step by step video, text & image solution for Cement, sand and seree are dropped in rotating cylidrical drum to make concrete mixture. If rotating speed of drum is very high then contents are attached to wall of drum and mixture is not formed correctly. If radius of drum is 1.25 m and its axis is horizontal, then the required maximum rotating speed to make good mixture in rpm is - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - MCQ
14 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
Similar Questions
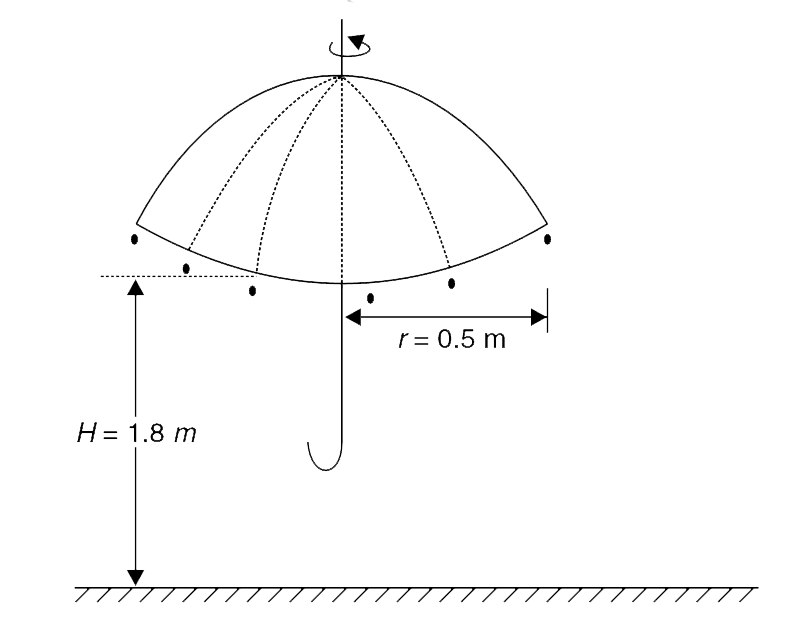
A wet umbrella is held upright (see figure). The man holding it is rotating it about its vertical shaft at an angular speed of ω=5 rad s–1. The rim of the umbrella has a radius of r=0.5 m and it is at a height of H=1.8 m from the floor. The man holding the umbrella gradually increases the angular speed to make it 2ω. Calculate the area of the floor that will get wet due to water drops spun off the rim and hitting the floor. [g=10m/s2].
View SolutionA 70kg man stands in contact against the inner wall of a hollw cylindrical drum of radius 3m rotating about its verticle axis. The coefficient of friction between the wall and his clothing nis 0.15 . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
View Solution
Knowledge Check
A uniform disc of radius a and mass m, is rotating freely with angular speed ω in a horizontal plane. About a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddently attached to the rim of the disc of the disc and rotates with it. The new angular speed is
Aω6Bω3Cω2Dω5A person stands in contact against a wall of cylindrical drum of radius 'r' rotating with an angular velocity ω. If μ is coefficient ofn static fiction between the wall and the person , then the minimum rotational speed which enables the person to remain struck to the wall will be
A√gμrB√μrgC√2gμrD√grμA uniform disc of radius 'a' and mass 'm' is rotating freely with angular speed ω in a horizontal plane about a smooth fixed vertical axis through its centre. A particle of mass 'm' is then suddenly attached to the rim of the disc and rotates with it. The new angular speed is
Aω/√3Bω/3Cω/√4Dω/5
Centrifuging may be used for the separation of isotopes. To do this a mixture of two gases is placed inside a cylindrical vessel rotating at a high speed. Because of the action of centrifugal forces, the isotope concentration near the cylinder wall will be different from that in the contre.
Compare the concentrations of the light and the heavy uranium isotopes near the centrifuge walls, if the diameter of the cylinder is 10 cm, the rotation speed is 2.0×103 r. p.s., the temperature of uranium hexafluoride is 27∘C. For concentrations in normal conditions see ξ25.6.
Find the enrichment factor in the mixture of the heavy isotope near the walls of the vessel. The term enrichment factor applies to the quotient obtained by dividing the concentration ratio during rotation by the initial concentration ratio:
x=(n2n1)(n02n01)
View SolutionA coin is placed at the edge of a horizontal disc rotating about a vertical axis through its axis with a uniform angular speed 2 rad s−1. The radius of the disc is 50 cm. Find the minimum coefficient of friction between disc and coin so that the coin does not slip. (Take g=10m/s2)
View SolutionA uniform disc of mass M and radius R is rotating freely about its central vertical axis with angular speed w0. Another disc of mass m and radius r is free to rotate about a horizontal rod AB. Length of the rod AB isL(<R) and its end A is rigidly attached to the vertical axis of the first disc. The disc of mass m, initially at rest, is placed gently on the disc of mass M as shown in figure. Find the time after which the slipping between the two discs will cease. Assume that normal reaction between the two discs is equal to mg. Coefficient of friction between the two discs is μ.

View SolutionA rod of mass m can rotate without friction about axis sliding (also without friction) along a conducting ring of radius b arranged in a vertical plane as shown in the . The entire arrengement is placed in a uniform magnetic field with the inducetion B perpendicular to the plane of the ring. The axis and the conductor are connected to teh terminals of a current source. Determine
(a) according to which law current I flowing in the rod must vary for the rod to rotate at a constant angular speed. Being to measure the time from the instant when the rod is in its right-hand horizontal position. Consider the current to be positive when it flows from the axis of rotation toward the ring.
(b) what emf E of the source must be applied to maintain the required current? Consider the total resistance of the circuit to be constant and equal to R. Disergard the inductance of teh circuit.

View Solution(a) Draw a schematic diagram of an AC generator. Explain is working and obtain the expression for the instantaneous value of the emf in terms of the magnetic field B, number of turns N of the coil of area A rotating with angular frequency ω. Show how an alternating emf is generated by loop of wire rotating in a magnetic field.
(b) A circular coil of radius 10 cm and 20 turns is rotated about its vertical diameter with angular speed of 50 rad s−1. in a uniform horizontal magnetic field of 3.0×10−2T.
(i) Calculate the maximum and average emf induced in the coil.
(ii) If the coil forms a closed loop of resistance 10Ω, calculate the maximum current in the coil and the average power loss due to Joule heating.
View Solution
