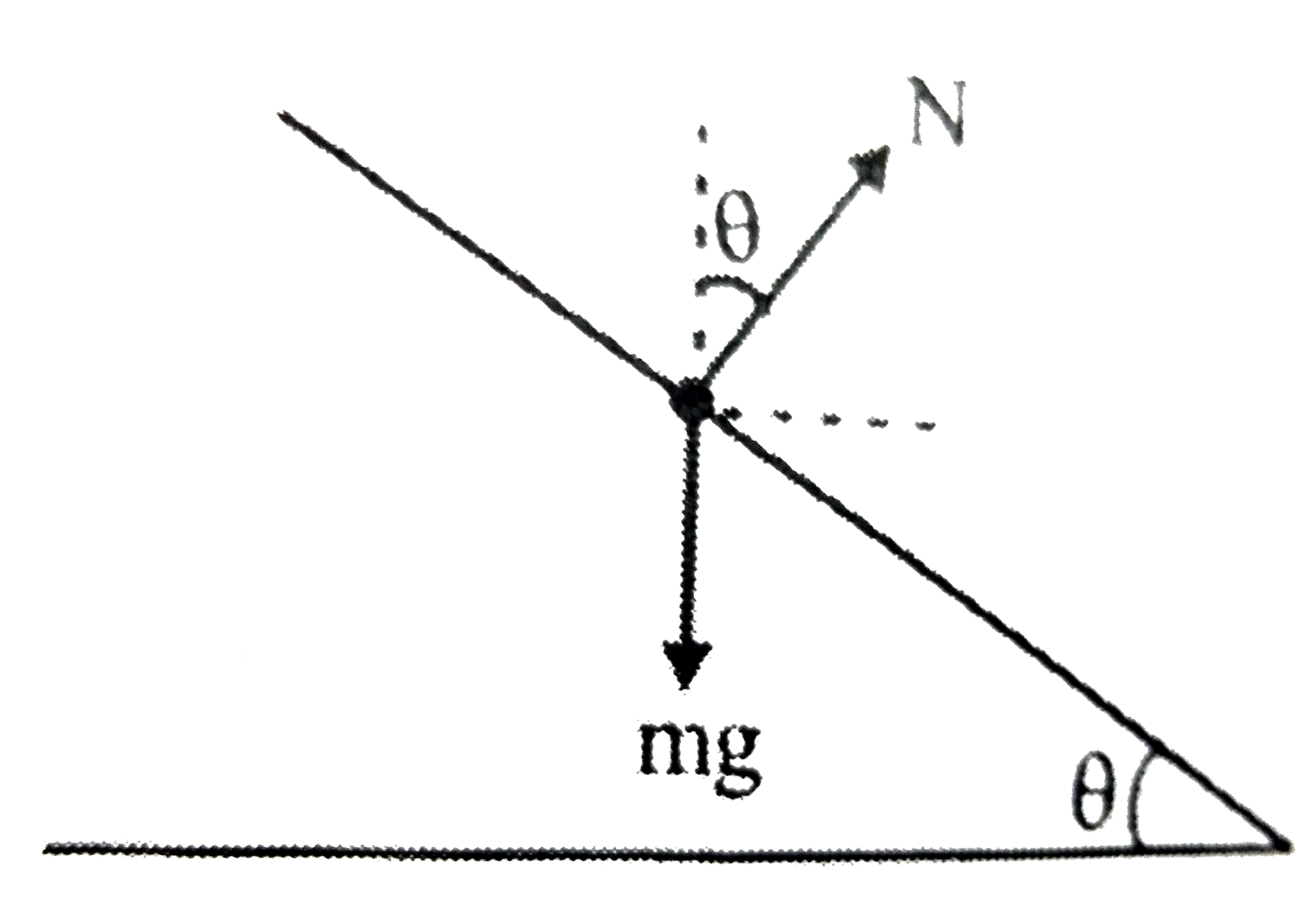
A car is moving along a banked road laid out as a circle of radius r . (a) What should be the banking angle θ so that the car travelling at speed v needs no frictional force from tyres to negotiate the turn ? (b) The coefficient of friction between tyres and road are μs=0.9 and μk=0.8 . At what maximum speed can a car enter the curve without sliding toward the top edge of the banked turn ?

Nsinθ=mv2randNcosθ=mg⇒tanθ=v2rg
NOTE: In above case friction does not play any role in negotiating the turn.
(b) If the driver moves faster than the speed mentioned above, a friction force myst act parallel to the road, inward towards center of the turn.
⇒Fcosθ+Nsinθ=mv2randNcosθ=mg+fsinθ
For maximum speed of f=μN
N(μcosθ+sinθ)=mv2randN(cosθ−μsinθ)=mg
=v2rg=sinθ+μcosθcosθ−μsinθ⇒v=√(sinθ+μcosθcosθ−μsinthea)rg

Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (S-1)
10 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - Dynamics of circular motion
8 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question
1 Video
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
Similar Questions
A car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tire and the road is μs=2.0, find the maximum speed the car can take without skidding.
View SolutionWhat is the maximum velocity with which a vehicle can negotiate a turn of radius r safely when coefficient of friction between tyres and road is μ ?
View Solution
Knowledge Check
The coefficient of friction between the tyres and the road is 0.25. The maximum speed with which a car can be driven round a curve of radius 40 m without skidding is (Take g=10ms−2)
A40ms−1B20ms−1C15ms−1D10ms−1The coefficient of friction between the tyres and the road is 0.25. The maximum speed with which a car can be driven round a curve of radius 40 m without skidding is (assume g=10ms−2)
A40ms−1B20ms−1C15ms−1D10ms−1Assuming the coefficient of friction between the road and tyres of a car to be 0.5, the maximum speed with which the car can move round a curve of 40.0 m radius without slipping, if the road is unbanked, should be
A25 m/sB19 m/sC14 m/sD11 m/s
The stopping distance for a vehicle of mass M moving with a speed v along a level road, will be - (µ is the coefficient of friction between tyres and the road)
View SolutionA car starts from rest on a 1600m long bridge. The coefficient of friction between the tyre and road is 0.8. The minimum time taken by the car to cross the bridge is
View SolutionA car is travelling along a curved road of radius r. If the coefficient of friction between the tyres and the road is μ the car will skid if its speed exceeds .
View SolutionA car is travelling at 36 kmph on a road . The maximum turning radius of the car is 20 m ans g=10m/s2 .Then the coefficient of friction between its tyres and the road is
View SolutionWhat would be the maximum speed of a car on a road turn of radius 30 m, if the coefficient of fraction between the types and the road is 0.4 ?
View Solution
