A function f: A to B whereA={a,b,c} , B={1,2,3,4}, How many function can be defined from A to B which are not one-one such that 2belongf(A)
The correct Answer is:A
To solve the problem of finding the number of functions from set A to set B that are not one-to-one and include the value 2 in their range, we can break it down into steps.
1. Identify the Sets:
- Let A={a,b,c} (3 elements)
- Let B={1,2,3,4} (4 elements)
2. Total Functions from A to B:
- The total number of functions from set A to set B is given by |B||A|.
- Here, |B|=4 and |A|=3.
- Thus, the total number of functions is 43=64.
3. Functions that are One-to-One:
- A one-to-one function from A to B can only be formed if the number of elements in A is less than or equal to the number of elements in B.
- The number of one-to-one functions can be calculated using permutations of the elements in B taken |A| at a time, which is P(4,3)=4!/(4−3)!=4!=24.
4. Functions that are Not One-to-One:
- To find the number of functions that are not one-to-one, we subtract the number of one-to-one functions from the total functions:
- Number of not one-to-one functions = Total functions - One-to-one functions = 64−24=40.
5. Functions that Include 2 in the Range:
- We need to ensure that the value 2 is included in the range of the functions.
- We can approach this by using complementary counting. First, we find the number of functions that do not include 2 in their range.
6. Functions Excluding 2:
- If we exclude 2 from B, we have B′={1,3,4} (3 elements).
- The total number of functions from A to B′ is 33=27.
7. Functions Including 2:
- The number of functions that include 2 in their range is then:
- Functions including 2 = Total functions - Functions excluding 2 = 64−27=37.
8. Final Count of Not One-to-One Functions Including 2:
- Now, we need to find the number of not one-to-one functions that include 2.
- From the previous step, we found that there are 40 not one-to-one functions in total, and 27 of these do not include 2.
- Therefore, the number of not one-to-one functions that include 2 is:
- Not one-to-one functions including 2 = Total not one-to-one functions - Not one-to-one functions excluding 2 = 40−27=13.
Conclusion:
The total number of functions from A to B that are not one-to-one and include the value 2 in their range is 13.
- Let A={a,b,c} (3 elements)
- Let B={1,2,3,4} (4 elements)
- The total number of functions from set A to set B is given by |B||A|.
- Here, |B|=4 and |A|=3.
- Thus, the total number of functions is 43=64.
- A one-to-one function from A to B can only be formed if the number of elements in A is less than or equal to the number of elements in B.
- The number of one-to-one functions can be calculated using permutations of the elements in B taken |A| at a time, which is P(4,3)=4!/(4−3)!=4!=24.
- To find the number of functions that are not one-to-one, we subtract the number of one-to-one functions from the total functions:
- Number of not one-to-one functions = Total functions - One-to-one functions = 64−24=40.
- We need to ensure that the value 2 is included in the range of the functions.
- We can approach this by using complementary counting. First, we find the number of functions that do not include 2 in their range.
- If we exclude 2 from B, we have B′={1,3,4} (3 elements).
- The total number of functions from A to B′ is 33=27.
- The number of functions that include 2 in their range is then:
- Functions including 2 = Total functions - Functions excluding 2 = 64−27=37.
- Now, we need to find the number of not one-to-one functions that include 2.
- From the previous step, we found that there are 40 not one-to-one functions in total, and 27 of these do not include 2.
- Therefore, the number of not one-to-one functions that include 2 is:
- Not one-to-one functions including 2 = Total not one-to-one functions - Not one-to-one functions excluding 2 = 40−27=13.
The total number of functions from A to B that are not one-to-one and include the value 2 in their range is 13.
Similar Questions
Knowledge Check
Given a function f:A→B, where A={1,2,3,4,5} and B={6,7,8}
Find number of all such functions y=f(x) which are one-one?A0B35C.5P3D53A function f:A→B is defined as :
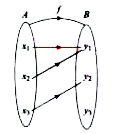
Which of the following is true ?Aone - one functionBone-one and onto functionCmany - one and into functionDmany-one and onto function
If A={1,2,3}, B={x,y} , then the number of functions that can be defined from A into B is 12 b. 8 c. 6 d. 3
View SolutionGiven : A={a,b,c,d} and B={1,2,3,4}.
Form ordered pairs showing a one - one function from A to B.
View SolutionThe number of one-one functions that can be defined from A={4,8,12,16} to B is 5040 then n(B)
View SolutionConsider set A{a,b,c,d,e} & set B{q,r,s}.Function f is defined from A to B.Find number of onto functions from A to B such that f(a)=q is?
View SolutionIf f:A→B,A={1,2,3,4},B={1,2,3} and f(i)≠i then the number of onto functions from A to B is
View SolutionIf d:A→B where A={2,3,4}andB{6,2,3,4,5}, then the number of non-decreasing functions on f that can be defined are ______
View Solution

