If temperature changes from 27∘C→42∘C then no. of molecules having energy greater than thershold energy become five times, then find activation energy of reaction in KJ. Given ln 5= 1.6094
The correct Answer is:84.30J
To find the activation energy of the reaction given the temperature change and the increase in the number of molecules with energy greater than the threshold energy, we can follow these steps:
Step 1: Convert temperatures from Celsius to Kelvin
- The initial temperature T1=27∘C=27+273=300K
- The final temperature T2=42∘C=42+273=315K
Step 2: Use the Arrhenius equation
The Arrhenius equation is given by:
k=Ae−EaRT
where:
- k is the rate constant,
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the universal gas constant (8.314 J/mol·K),
- T is the temperature in Kelvin.
Step 3: Relate the rate constants at two different temperatures
Given that the number of molecules with energy greater than the threshold energy becomes five times, we can express this as:
k2k1=5
Taking the natural logarithm of both sides:
ln(k2k1)=ln(5)
Thus,
ln(k2)−ln(k1)=ln(5)
Given ln(5)=1.6094.
Step 4: Substitute into the Arrhenius equation
From the Arrhenius equation, we can write:
ln(k2)=ln(A)−EaRT2
ln(k1)=ln(A)−EaRT1
Subtracting these two equations gives:
ln(k2)−ln(k1)=−EaRT2+EaRT1
Substituting ln(k2)−ln(k1)=ln(5):
1.6094=−EaRT2+EaRT1
Step 5: Rearranging the equation
Rearranging gives:
1.6094=EaR(1T1−1T2)
Substituting R=8.314J/mol⋅K:
1.6094=Ea8.314(1300−1315)
Step 6: Calculate 1T1−1T2
Calculating 1300−1315:
1300=0.003333K−1
1315=0.003175K−1
Thus,
1300−1315=0.003333−0.003175=0.000158K−1
Step 7: Substitute back to find Ea
Substituting back into the equation:
1.6094=Ea8.314⋅0.000158
Rearranging gives:
Ea=1.6094⋅8.3140.000158
Calculating this gives:
Ea=13.3790.000158≈84666.46J/mol
Converting to kJ:
Ea≈84.67kJ/mol
Final Answer
The activation energy Ea is approximately 84.67 kJ/mol.
- The initial temperature T1=27∘C=27+273=300K
- The final temperature T2=42∘C=42+273=315K
The Arrhenius equation is given by:
k=Ae−EaRT
where:
- k is the rate constant,
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the universal gas constant (8.314 J/mol·K),
- T is the temperature in Kelvin.
Given that the number of molecules with energy greater than the threshold energy becomes five times, we can express this as:
k2k1=5
Taking the natural logarithm of both sides:
ln(k2k1)=ln(5)
Thus,
ln(k2)−ln(k1)=ln(5)
Given ln(5)=1.6094.
From the Arrhenius equation, we can write:
ln(k2)=ln(A)−EaRT2
ln(k1)=ln(A)−EaRT1
Subtracting these two equations gives:
ln(k2)−ln(k1)=−EaRT2+EaRT1
Substituting ln(k2)−ln(k1)=ln(5):
1.6094=−EaRT2+EaRT1
Rearranging gives:
1.6094=EaR(1T1−1T2)
Substituting R=8.314J/mol⋅K:
1.6094=Ea8.314(1300−1315)
Calculating 1300−1315:
1300=0.003333K−1
1315=0.003175K−1
Thus,
1300−1315=0.003333−0.003175=0.000158K−1
Substituting back into the equation:
1.6094=Ea8.314⋅0.000158
Rearranging gives:
Ea=1.6094⋅8.3140.000158
Calculating this gives:
Ea=13.3790.000158≈84666.46J/mol
Converting to kJ:
Ea≈84.67kJ/mol
The activation energy Ea is approximately 84.67 kJ/mol.
Similar Questions
Knowledge Check
An endothermic reaction A → B has an activation energy as × kJ mo1−1 of A. If energy change of the reaction is y kJ, the activation energy of the reverse reaction is :
A−xBx - yCx + yDy - xA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
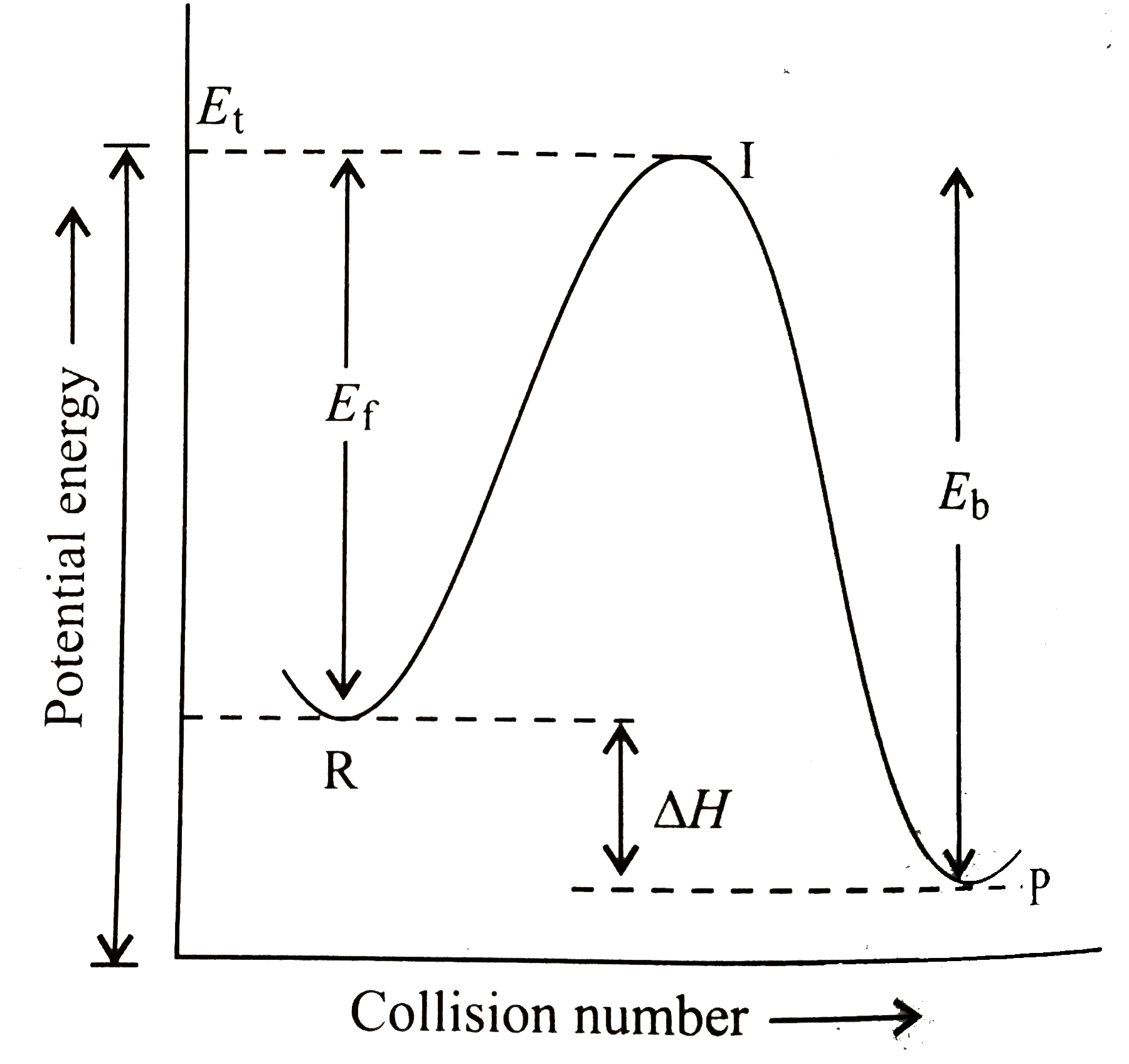
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
If a reaction A+B→C is exothermic to the extent 30kJmol−1 and the forward reaction has an activation energy of 249kJmol−1 the activation energy for reverse reaction in kJmol−1 isA324B279C40D100For the bimolecular gaseour reaction:
2R(g) → Products, the fraction of molecules having sufficient energy for effective collision is 2.06×10−9 at 127∘ C. The activation energy for reaction is about (ln 2.06 = 0.727, ln 10 = 2.303) .A16 kJ/moleB16 kcal/moleC8 kcal/moleD80 kcal/moile
The reaction A+B→C+D+40KJ has activation energy of "18KJ" .Then the activation energy for the reaction C+D→A+B is
View SolutionThe number of molecules with energy greater than tha threshold enegy for a reaction increases five fold by a rise of temperature from 27∘C to 42∘C. Its energy of activation in J/mol is ___________. (Take ln5=1.6094,R=8.314 J mol−1K−1)
View SolutionThe rate of a reaction triples when temperature change from 20∘C to 50∘C . Calculate the energy of activation.
View SolutionIf a reaction A + B → C, is exothermic to the extent of 30 kJ/mol and the forward reaction has an activation energy of 249 kJ/mol, the activation energy for reverse reaction in kJ/mol is
View SolutionThe rate of a reaction quadruples when the temperature changes from 300 to 310 K. The activation energy of this reaction is :
( Assume Activation energy and pre-exponential factor are independent of temperature, ln(2)=0.693,R=8.314J−mol−1K−1)
View Solution
