A block of mass m start slipping from top of inclined plane at B and comes to rest when reaches to lowest point A of inclined plane, if BC = 2AC and friction coefficient of part AC is 'mu = ktan(theta)' then find value of k 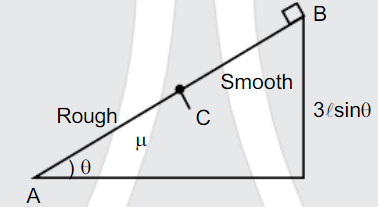
2
43832
3
43833
The correct Answer is:C
Step by step video, text & image solution for A block of mass m start slipping from top of inclined plane at B and comes to rest when reaches to lowest point A of inclined plane, if BC = 2AC and friction coefficient of part AC is 'mu = ktan(theta)' then find value of k by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle starts from rest from the top of an inclined plane and again comes to rest on reaching the bottom most point of the inclined plane. If the coefficient of friction on some part of inclined plane is 3tanθ and rest portion is smooth then the ratio of the rough length of the inclined to smooth length is 1:n1 then value of n is .....?
View Solution
A small back starts slipping down from a point B on an inclined plane AB, which is making an angle θ with the remaining section CA is rough with a coefficient of friction μ. It is found that bottom (point A) of the inclined plane. If BC=2AC, the coefficient of friction is given by μ=Ktanθ
The value of K is ________.
View Solution
Knowledge Check
A block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
AmgBmg sin θCμmgcosθDμmgsinθA body of mass m starts sliding down an incline of 30∘ from rest. The body comes to rest just when it reaches the bottom. If the top half of the plane is perfectly smooth and the lower half is rough, find the force of friction :
Amg4Bmg√3CmgDmg√2A block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
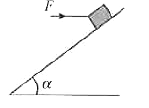 ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
If the body starts from rest from the top of the rough inclined plane of length 1, time taken to reach the bottom of the plane is
View SolutionA block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
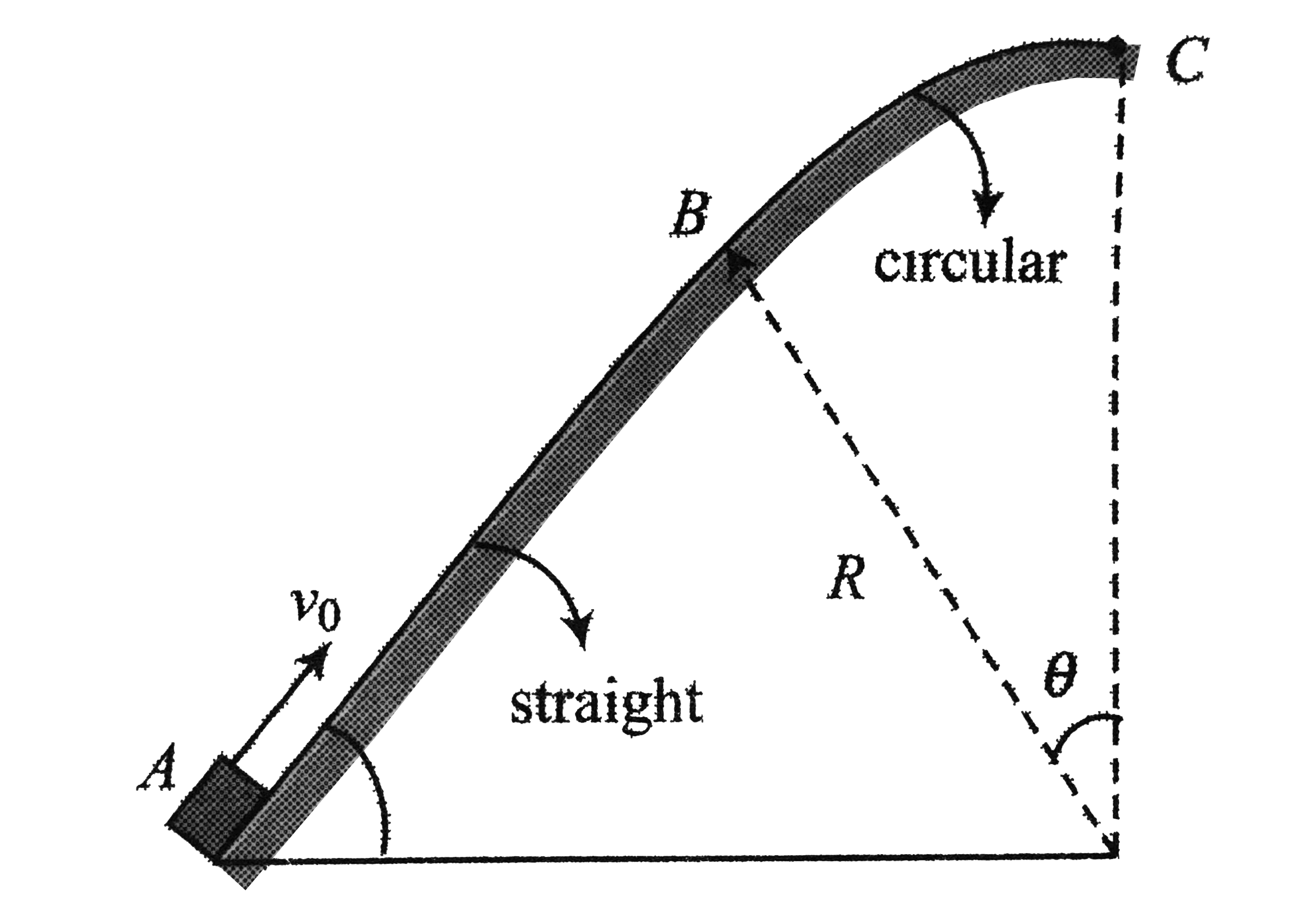
View Solution
A block is released from the top of the smooth inclined plane of height h. Find the speed of the block as it reaches the bottom of the plane.
View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View SolutionA block of mass m slides from the top of an inclined plane of angle of inclination θ & length l. The coefficient of friction between the plane and the block is μ. Then it is observed over a distance d along the horizontal surface having the same coefficient of friction μ, before it comes to a stop. Find the value of d.
View Solution
