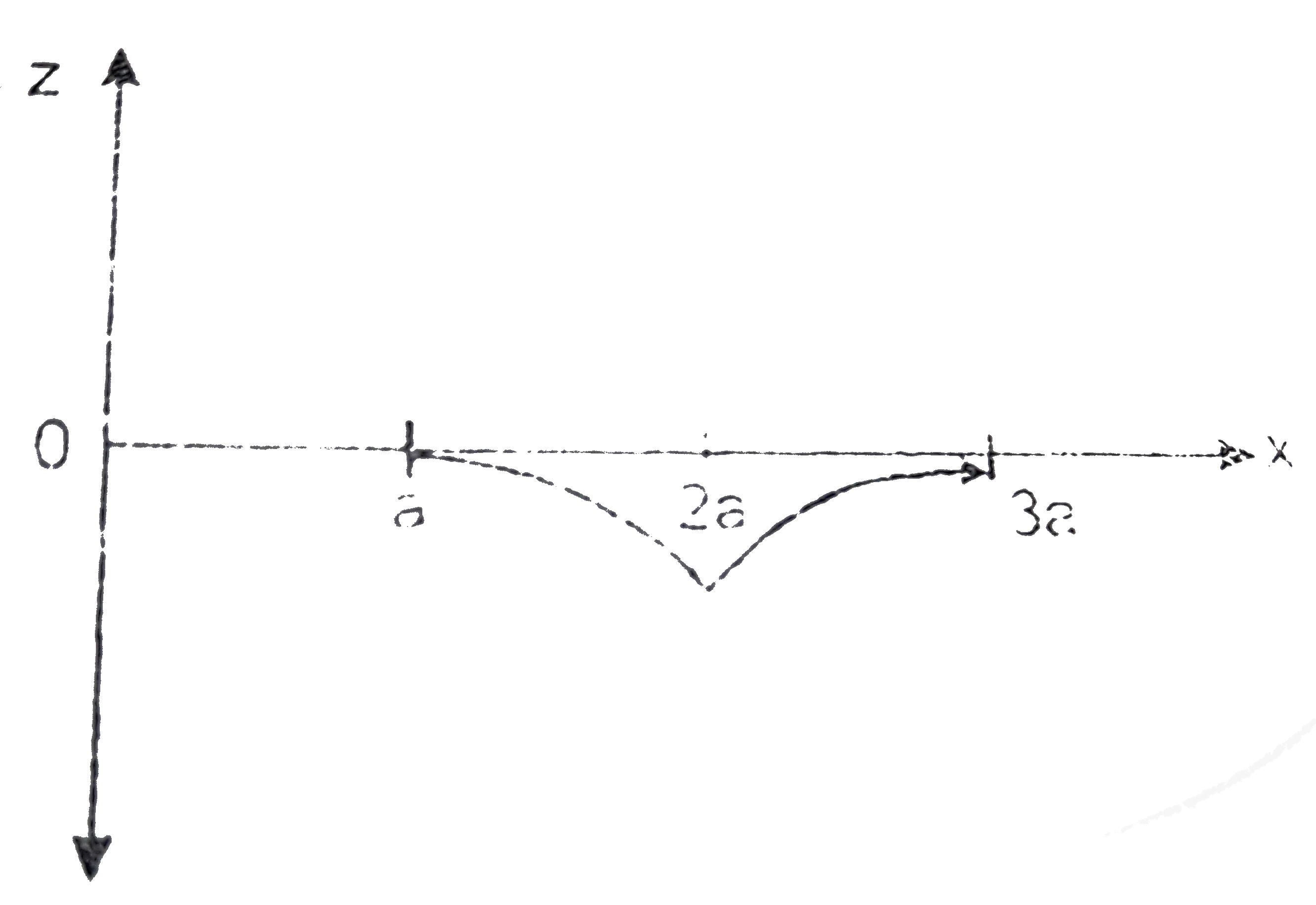
A magnetic field →B=B0ˆj , exists in the region a<x<2a , and →B=−B0ˆj , in the region 2a<x<3a, where B0 is a positive constant . A positive point charge moving with a velocity →v=v0ˆi , where v0 is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like




The correct Answer is:A
Magnitic field in the region a<x<2a will turn the particle towards positive Z-axis while the magnetic field in the region 2a<x<3a will exert force in opposite direction.The turning is smooth because the magnetic force is NOT impulsive.
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-3 PART-2
27 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-3 PART-3
29 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3 COMPREHENSION- 3
5 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
A magnetic field →B=−B0ˆi exists within a sphere of radius R=v0T√3 where T is the time period of one revolution of a charged particle starting its motion form origin and moving with a velocity vce(v)0=v02√3ˆi−v02ˆj. Find the number of turns that the particle will take to come out of the magnetic field.
View SolutionAn alpha particle moving with the velocity →v=uˆi+ˆj ,in a uniform magnetic field →B=Bˆk . Magnetic force on alpha particle is
View Solution
Knowledge Check
A magnetic field →B=B0ˆj exists in the region a<x<2a and →B=−B0ˆi in the region 2a<x<3a, where B0 is positive constant. A positive point charge moving with a velocity →v=v0ˆi where v0 is a positive constant, enters.
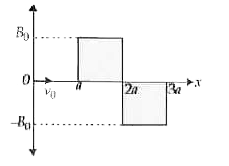
the magnetic field at x=a, The trajectory of the charge in this region can be like,A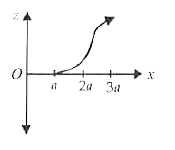 B
B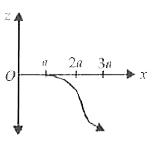 C
C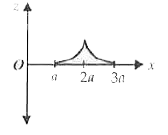 D
D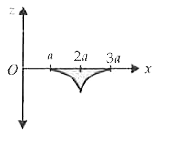
A portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
Aits z co-ordinate can never be negativeBits x co-ordinate can never be positiveCits x and z co-oridinate cannot be zero at the same timeDits y co-ordinate will be proportional to its time of flightIn region x>0 a uniform and constant magnetic field →B1=2B0ˆk exists. Another uniform and constant magnetic field →B2=B0ˆk exists in region x<0 A positively charged particle of mass m and charge q is crossing origin at time t =0 with a velocity ¯u=u0ˆi. The particle comes back to its initial position after a time : (B0,u0 are positive constants)
A32πmqB0B2πmqB0C3πmqB0DParticle does not come back to its initial position
There exists a uniform magnetic field →B=+B0ˆk for x>0and→B=0 for all x<0. A charged particle placed at (0,−a,0) is given an initial velocity →v=v0ˆi. What is the magnitude and nature of charge on the particle such that it crosses through the origin ?
Strategy: When the charge is projected perpendicular to a uniform magnetic field, it follows a circular path. In this case, the force acting on it will be directed either towards +y-axis. or y-axis. It is given that it crosses point O. Thus, the force at (0,−a,0) must be towards y-axis
View SolutionIn a region of space , suppose there exists a uniform electric field →E=10ˆi(Vm) . If a positive charge moves with a velocity →v=−2ˆj, its potential energy
View SolutionA charged particle moves with velocity →v=aˆi+dˆj in a magnetic field →B=Aˆi+Dˆj. The force acting on the particle has magnitude F. Then,
View SolutionFind the potential V of an electrostatic field →E=a(yˆi+xˆj), where a is a constant.
View SolutionFigure shows sqare current caarrying coil of edge lengthL. The magnetic field on the coil is given by →B=B0yLˆi+B0xLˆj where B0 is a positive constant.

View Solution
