A constant direct current of uniform density ˆj is flowing in an infinitely long cylindrical conductor.The conductor contains an infinitely long cylindrical cavity whose axis is parallel to that of the conductor and is a a distance →l from it.What will be the magnetic induction →B at a point inside the cavity at a distance →r from the centre of cavity?
μ0(→j×→r)2
μ0(→j×→l)2
μ0(→j×→l)+μ0(→j×→r)2
μ0(→j×→l)−μ0(→j×→r)2
The correct Answer is:B
B=μ02[→J×(→l+→r)]+μ02[−→J×→r]
→B=μ02[→J×→l]

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-1
15 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-2
26 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-1
81 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
Inside a long staight unifrom wire of round cross-section there is a long round cylindrical cavity whose axis is parallel to the axis of the wire and displaced from the latter by a distance 1. A direct current of density j flows along the wire. Find the magnedtic induction inside the cavity. Consider, in particular , the case l=0.
View SolutionInside a long straight uniform wire of round cross-section, there is a long round cylindrical cavity whose axis is parallel to the axis of the wire and displaced from the latter by a distance l. A direct current of density j flows along the wire. Find the magnetic induction inside the cavity. Consider, in particular, the case l=0.

View Solution
Knowledge Check
A current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor of the cable, then the magnetic induction at any point outside the conductor at a distance r meter from the axis is
A∞BZeroCμ04π2irDμ04π2πrrThe magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
A|B|=(μ04π)2irB|B|=(μ04π)r2iC|B|=(4πμ0)2irD|B|=(4πμ0)r2i
An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-AρR6ε0BρR4ε0CρR2ε0DρR3ε0
The uniform current flowing through a thin hollow cylindrical conductor is I. What is the magnetic field inside the cylinder?
View SolutionA very long straight conductor has a circular cross- section of radius R and carries a current density J. Inside the conductor there is a cylindrical hole of radius a whose axis is parallel to the axis of the conductor and a distance b from it. Let the z-axis be the axis of the conductor, and let the axis of the hole be at x = b. Find the magnetic field
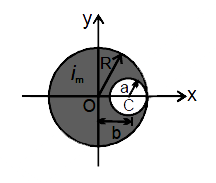
on the y = axis at y = 2R.
View SolutionA very long straight conductor has a circular cross- section of radius R and carries a current density J. Inside the conductor there is a cylindrical hole of radius a whose axis is parallel to the axis of the conductor and a distance b from it. Let the z-axis be the axis of the conductor, and let the axis of the hole be at x = b. Find the magnetic field
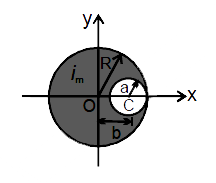
on the x=axis at x = 2R
View SolutionA steady current I flows along an infinitely long straight wire with circular cross-section of radius R. What will be the magnetic field outside and inside the wire at a point r distance far from the axis of wire?
View SolutionFor a given distance from a current element, the magnetic induction is maximum at an angle measured with respect to axis of the current carrying conductor.
View Solution
