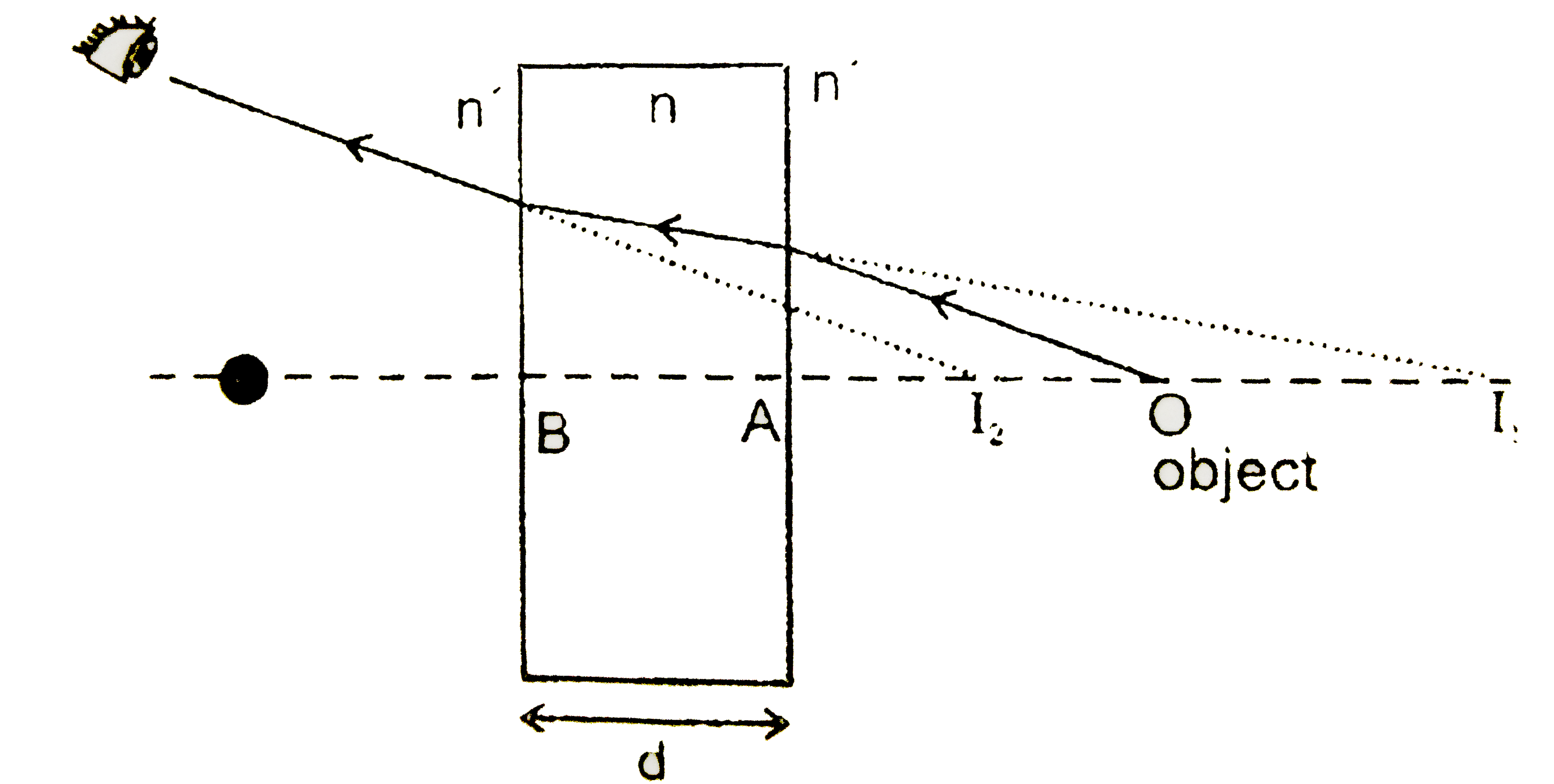
Prove that the shift in position of object due to parallel slab is given by shift
=d(1−1nnet) where nrel=nn'

Video Solution
Text Solution
Because of the way refraction at the first surface, the image of O is formed at l1. For this refraction the real depth is AO=x and apparent depth is AI1
Thus Al1=AOni/nr=AOn'/n=n(AO)n'
The point l1 acts as the object for the refractin fo secound surface. Dua to this refraction, the image pf l1 is formed at l2 Thus,
Bl2=(Bl1)(n/n')=n'n(bl1)
=n'/n[d+nn'(AO)]=n'nd+AO.
Net shift =Oi2=BO−Bl2
=d+(AO)−n'nd−AO=d(1−n'n)=d(1−1nrel) where nrel=nn'
|
Topper's Solved these Questions
- GEOMATRICAL OPTICS Book:RESONANCEChapter:GEOMATRICAL OPTICS Exercise:Exercise-1
Explore 142 Videos
- GEOMATRICAL OPTICS Book:RESONANCEChapter:GEOMATRICAL OPTICS Exercise:Exercise-2
Explore 63 Videos
- GEOMATRICAL OPTICS Book:RESONANCEChapter:GEOMATRICAL OPTICS Exercise:Advance level Problems
Explore 35 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCEChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
- GRAVITATIONBook:RESONANCEChapter:GRAVITATIONExercise:HIGH LEVEL PROBLEMS
Explore 16 Videos
Similar Questions
Knowledge Check
The lateral shift produced due to parallel sided glass slab depends on
Aangle of incidenceBthickness of the glass slabCthe refarctive index of the material of the slabDall of these
Prove that the function f(x)=xnis continuous at x=n, where n is a positive integer.
View SolutionProve that (n!)! is divisible by (n!)(n−1)!
View SolutionIf n ≥ 1 is a positive integer, then prove that 3n≥2n+n.6n−12
View SolutionProve that the number of ways to select n objects from 3n objects of whilch n are identical and the rest are different is 22n−1+(2n)!2(n!)2
View SolutionProve that for every positive integer n,1n+8n−3n−6nis divisible by 10.
View SolutionIf n2−11n+24=0 is satisfied by n1&n2 where n2>n1 then
View SolutionProve that [n+1/2]n>(n!).
View Solution
