Show that the factor (1R1−1R2) (and therefore focal length) does not depend on which surface of the lens strike first.
Consider a convex lens of radii of curvature p and q as shwon.
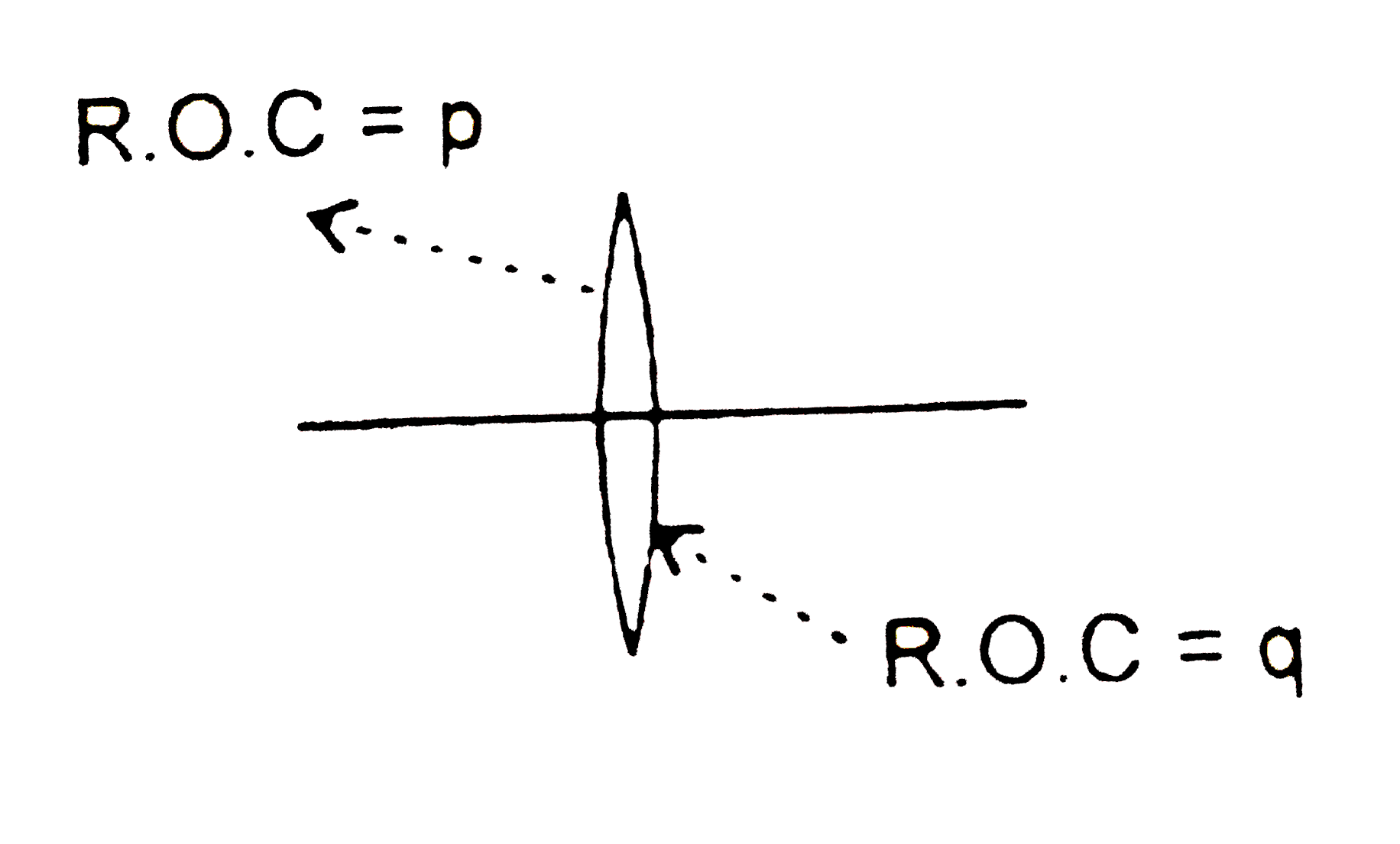
Case 1: Suppose light is incident form left side and strikes the surface with radius of curvature p, first,
Then R1=+p,R2=−q and (1R1−1R2)=(1p−1−q))
CASE 2: Suppose light is incident form right side and strikes the surface with radius of curvature q, first.
Then R1=+q,R2=−p and ((1)/(R_(1)) - (1)/(R_(2))) = ((1)/(q) - (1)/(-p)))
Though we have shwon the result for biconvex lens, it is true for every lens.
Topper's Solved these Questions
- GEOMATRICAL OPTICS Book:RESONANCEChapter:GEOMATRICAL OPTICS Exercise:Problem
Explore 33 Videos
- GEOMATRICAL OPTICS Book:RESONANCEChapter:GEOMATRICAL OPTICS Exercise:Exercise-1
Explore 142 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCEChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
- GRAVITATIONBook:RESONANCEChapter:GRAVITATIONExercise:HIGH LEVEL PROBLEMS
Explore 16 Videos
Similar Questions
Name two factors on which the focal length of a lens depends.
View SolutionStatement-1 : A glass convex lens (refractive index, μ1=1.5), when immersed in a liquid of refractive index μ2=2, functions as a diverging lens.
Statement-2 : The focal length of a lens is given by 1f=(μ−1)(1R1−1R2), where μ is the relative refractive index of the material of the lens with respect to the surrounding medium.
View Solution
Knowledge Check
The focal length of a lens is 0.1 m. Then the lens must be
AconvexBconcaveCcylindricalDnone of thesePower of a lens of focal length 1 cm is
A1DB10DC100 DD1100D
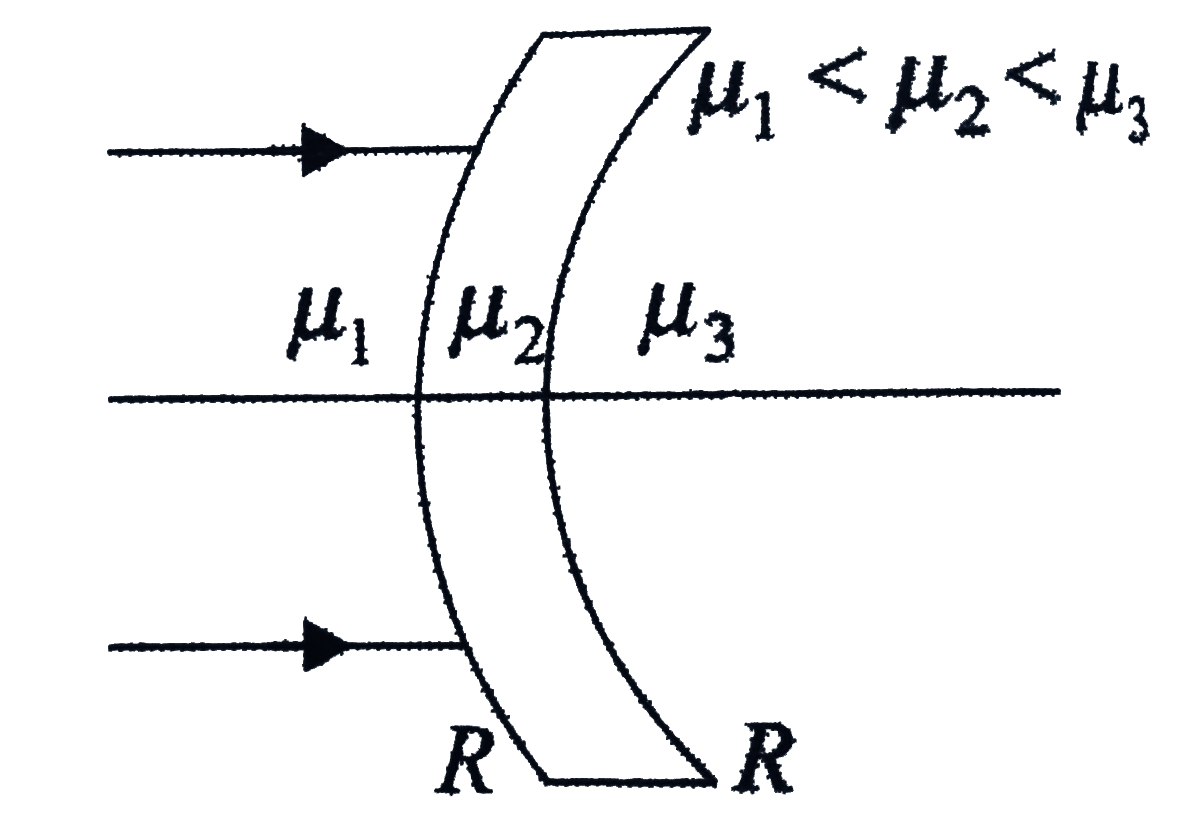
Find the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
View Solutionshow that r2r3+r3r1+r1r2=s2
View SolutionOn what factors does the focal length of a spherical mirror depend ?
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
Let the given biconvex lens be divided in two equal parts, as shown in Fig. (a), along a section YY' which is perpendicular to the principal axis of lens. What is the power of each part?

View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
How is your answer modified if the given biconvex lens is divided into two parts along a section XX' along its principal axis ?
View SolutionLens maker's formula is a formula corelating the power P (or focal length f) of a lens to radii of curvature of the two surfaces of the lens and the refractive index of lens material with respect to its surroundings. The formula is expressed as :
P=1f=(n−1)(1R1−1R2)
where n = refractive index of the material of lens with respect to its surroundings (ordinarily air) and R1andR2 are the radii of curvature of two surfaces of the lens. The relation is true under all conditions but while applying it we should put values of P, f, R1andR2 with their proper signs as per sign convention being followed by us.
Let us have a bi- convex lens and let radii of curvature of both its curved surfaces is same i.e., |R1|=|R2|=R (say)
If two lens parts obtained in (b) are joined together as shown in Fig. (c), (i) what is the net power of the combination?
View Solution
