For a prism, A=60∘,n=√7/3 . Find the minimum possible angle of incidence, so that the light ray is refracted from the second surface. Also, find δmax.
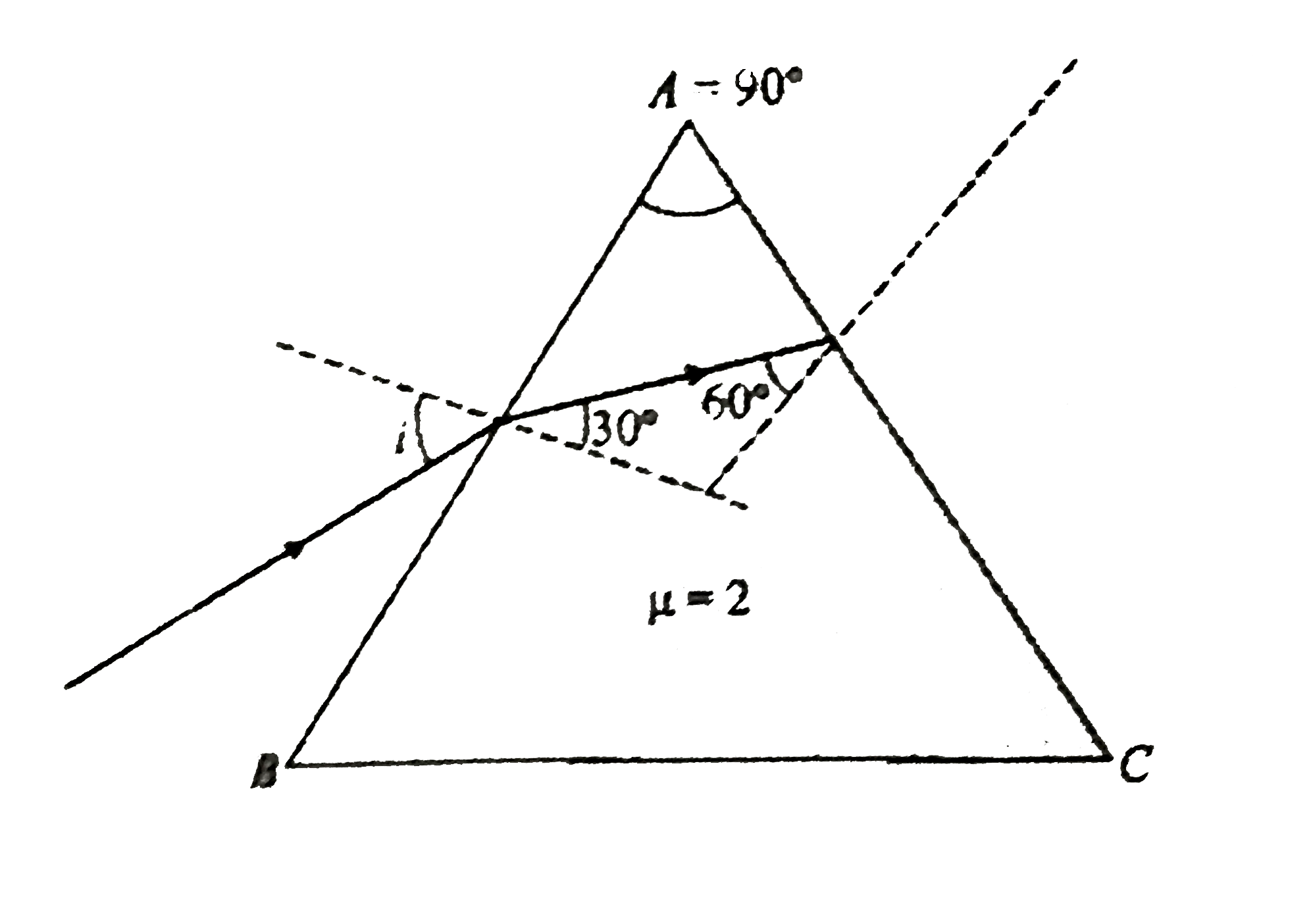
In minimum incidence case the angles will be as shwon in figure
Applying snell's law:
x×sinimin=√73sin(A−C)
=√73(sinAcosC−cosAsinC)
=√73(sin60√1−37−cos60√37)=12
∴imin=30∘,∴δmax=imax+90∘−A=30∘+90∘−60∘=60∘

Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Problem
33 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-1
142 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
A prism (n=2) of apex angle 90∘ is palced in air (n=1). What should be the angle of incidence so that light ray strikes the second surface at an angle of incidence 60∘.
View SolutionIn figure shown find the angle of incidence of the light ray on face AB of the prism for which light will reach face AC at incidence angle 60∘.
[90∘]
View Solution
Knowledge Check
Light ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
Asin−1(√3−12)Bsin−1(√2−12)Csin−1(√32)Dsin−1(23√3)Light ray is incident on a prism of angle A=60∘and refractive indexμ=√2.the angle of incidence at which the emergent ray grazes the surface is given by
Asin−1(√3−12)Bsin−1(1−√32)Csin−1(√32)Dsin−1(2√3)Refractive index of a prism is √7/3 and the angle of prism is 60∘. The minimum angle of incidence of a ray that will be transmitted through the prism is
A30∘B45∘C15∘D50∘
In an isosceles prism of prism angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergent ray grazes the emergent surface. Find the refractive index of the material of the prism.For what angle of incidence the angle of deviation will be minimum ?
View SolutionA light ray incidents on an equilateral triangle with an angle of 30∘. Find the angle of deviation of the emergent light ray if the angle of emergence from the second surface is 70∘.
View SolutionA prism of refractive index √2 has refractive angle 60∘ . Find the angle of incidence so that a ray minimum deviation.
View Solution(a) If the refracting angle of a prism is 60∘ and the minimum deviation is 30∘, then find the angle of incidence.
(b) A ray of light passes through an equilateral prism such that the angle of emergence is equal to the angle of incidence and each is equal to 3/4th of the angle of prism. Find the angle of deviation.
(c) The refracting of a prism is A and the refractive index of the material of the prism is cotA/2. Find the angle of deviation.
(d) The angle of a prism is 60∘. What is the angle of incidence for minimum deviation? The refractive index of the material of the prism is √2.
View SolutionIn a condition of minimum deviation μ=√3. Angle of incidence = 2 x angle of refraction then find angle of prism.
View Solution
