Question

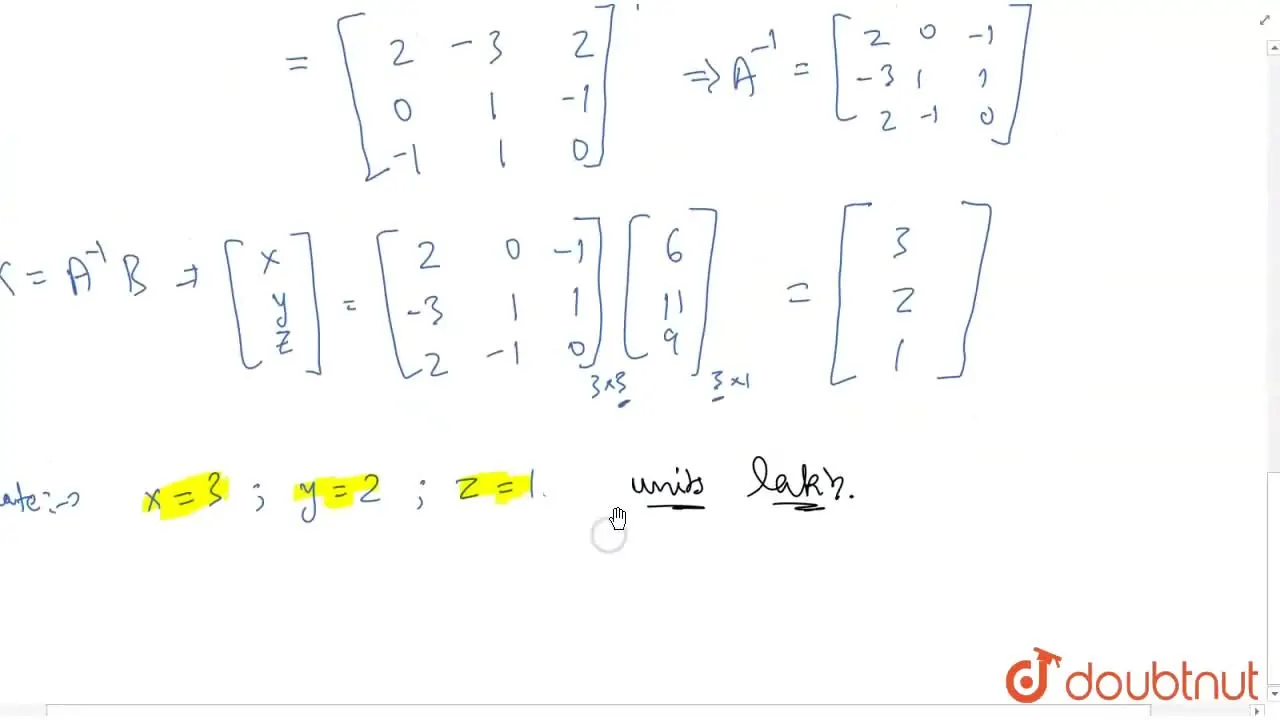
Two cricket teams honored their players for three values, excellent batting, to the point bowling and unparalleled fielding by giving Rs x, Rs y and Rs z per player respectively. The first team paid respectively 2, 2 and 1 players for the above values with a total money of 11 lakhs, while the second team paid respectively 1,2 and 2 players for these values with a total prize money of Rs. 9 lakhs. If the total award money for one person each for these values amount to Rs.6 lakhs, then express the above situation as a matrix equation and find award money per person for each value.

Answer

Excellent batting: 3 lakhs
point bowling: 2 lakhs
fielding: 1 lakh

Explanation

To solve the given problem, we will express the situation as a matrix equation and then find the award money per person for each value. Let's break it down step by step.

Step 1: Define the Variables
Let:
- \( x \) = award money for excellent batting (in lakhs)
- \( y \) = award money for to-the-point bowling (in lakhs)
- \( z \) = award money for unparalleled fielding (in lakhs)

Step 2: Set Up the Equations
From the problem statement, we can derive the following equations based on the payments made by the two teams:

1. For Team A:
- 2 players for batting: \( 2x \)
- 2 players for bowling: \( 2y \)
- 1 player for fielding: \( 1z \)
- Total amount paid = 11 lakhs
- Equation: \( 2x + 2y + z = 11 \)

2. For Team B:
- 1 player for batting: \( 1x \)
- 2 players for bowling: \( 2y \)
- 2 players for fielding: \( 2z \)
- Total amount paid = 9 lakhs
- Equation: \( x + 2y + 2z = 9 \)

3. Total Award Money:
- Total award money for one person each for these values = 6 lakhs
- Equation: \( x + y + z = 6 \)

Step 3: Write the Matrix Equation
We can express the above equations in matrix form \( AX = B \):

\( A = \begin{bmatrix} 2 & 2 & 1 \\ 1 & 2 & 2 \\ 1 & 1 & 1 \end{bmatrix}, \quad X = \begin{bmatrix} x \\ y \\ z \end{bmatrix}, \quad B = \begin{bmatrix} 11 \\ 9 \\ 6 \end{bmatrix} \)

Thus, the matrix equation is:

\( \begin{bmatrix} 2 & 2 & 1 \\ 1 & 2 & 2 \\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 11 \\ 9 \\ 6 \end{bmatrix} \)

Step 4: Find the Inverse of Matrix A
To solve for \( X \), we need to find \( A^{-1} \) and then compute \( X = A^{-1}B \).

1. Calculate the Determinant of A:
\( \text{det}(A) = 2(2 \cdot 1 - 2 \cdot 1) - 2(1 \cdot 1 - 2 \cdot 1) + 1(1 \cdot 2 - 2 \cdot 1) = 2(0) - 2(-1) + 1(0) = 2 \)

Since the determinant is not zero, the inverse exists.

2. Calculate the Adjoint of A:
The adjoint of matrix \( A \) is calculated using the cofactors and then transposing the matrix.

\( A^{-1} = \frac{1}{\text{det}(A)} \cdot \text{adj}(A) \)

After calculating the cofactors and transposing, we find:

\( A^{-1} = \begin{bmatrix} 2 & 0 & -1 \\ -3 & 1 & 1 \\ 2 & -1 & 0 \end{bmatrix} \)

Step 5: Multiply \( A^{-1} \) by \( B \)
Now, we compute \( X = A^{-1}B \):

\( X = \begin{bmatrix} 2 & 0 & -1 \\ -3 & 1 & 1 \\ 2 & -1 & 0 \end{bmatrix} \begin{bmatrix} 11 \\ 9 \\ 6 \end{bmatrix} \)

Calculating the multiplication:

1. First row: \( 2 \cdot 11 + 0 \cdot 9 - 1 \cdot 6 = 22 - 6 = 16 \)
2. Second row: \( -3 \cdot 11 + 1 \cdot 9 + 1 \cdot 6 = -33 + 9 + 6 = -18 \)
3. Third row: \( 2 \cdot 11 - 1 \cdot 9 + 0 \cdot 6 = 22 - 9 = 13 \)

Thus, we have:

\( X = \begin{bmatrix} 3 \\ 2 \\ 1 \end{bmatrix} \)

Step 6: Conclusion
The award money per person for each value is:
- \( x = 3 \) lakhs (excellent batting)
- \( y = 2 \) lakhs (to-the-point bowling)
- \( z = 1 \) lakh (unparalleled fielding)