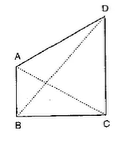
In figure $O A * O B = O C * O D$ . Show that $∠ A = ∠ C$ and $∠ B = ∠ D$ .

Video Solution

Text Solution

Verified by Experts

Here, we are given,
$O A * O B = O C * O D$
Dividing both sides by $O B * O C$ , we get,
$\frac{O A}{O C} = \frac{O D}{O B}$
Also, $∠ A O D = ∠ B O C$
So, by Side-Angle-Side Similarity rule,
$Δ A O D ~ Δ C O B$
That means, $∠ A = ∠ C and ∠ B = ∠ D$

Updated on:21/07/2023

|

Class 10 MATHS TRIANGLES

Similar Questions

In figure $O A * O B = O C * O D$ . Show that $∠ A = ∠ C$ and $∠ B = ∠ D$ .
View Solution
In Figure, $A B$ and CD are respectively the smalles and longest sides of a quadrilateral $A B C D .$ Show that $∠ A > ∠ C$ and $∠ B > ∠ D .$

View Solution
In Figure, $A B a n d C D$ are respectively the smallest and longest sides of a quadrilateral $A B C D .$ Show that $∠ A > ∠ C a n d ∠ B > ∠ D$

View Solution
In Fig. 4.126, $\frac{O A}{O C} = \frac{O D}{O B}$ . Prove that $∠ A = ∠ C$ and $∠ B = ∠ D$ . (FIGURE)
View Solution
In Figure, $A B C D$ is a trapezium in which $A B C D$ and $A D = B C .$ show that : $∠ A = ∠ B$ (ii) $∠ C = ∠ D$ $A B C ≅ B A D$ diagonal $A C = d i a g o n a l B D$
View Solution
In the given figure, $∠ B < ∠ A and ∠ C < ∠ D .$ Show that $A D < B C .$
View Solution
In a $A B C, ∠ A B C = ∠ A C B$ and the bisectors of $∠ A B C a n d ∠ A C B$ intersect at $O$ such that $∠ B O C = 120^{0} .$ Show that $∠ A = ∠ B = ∠ C = 60^{0}$ .
View Solution
In figure, $Δ O D C Δ O B A, ∠ B O C = 125^{o}$ and $∠ C D O = 70^{o}$ . Find $∠ D O C, ∠ D C O and ∠ O A B$ .
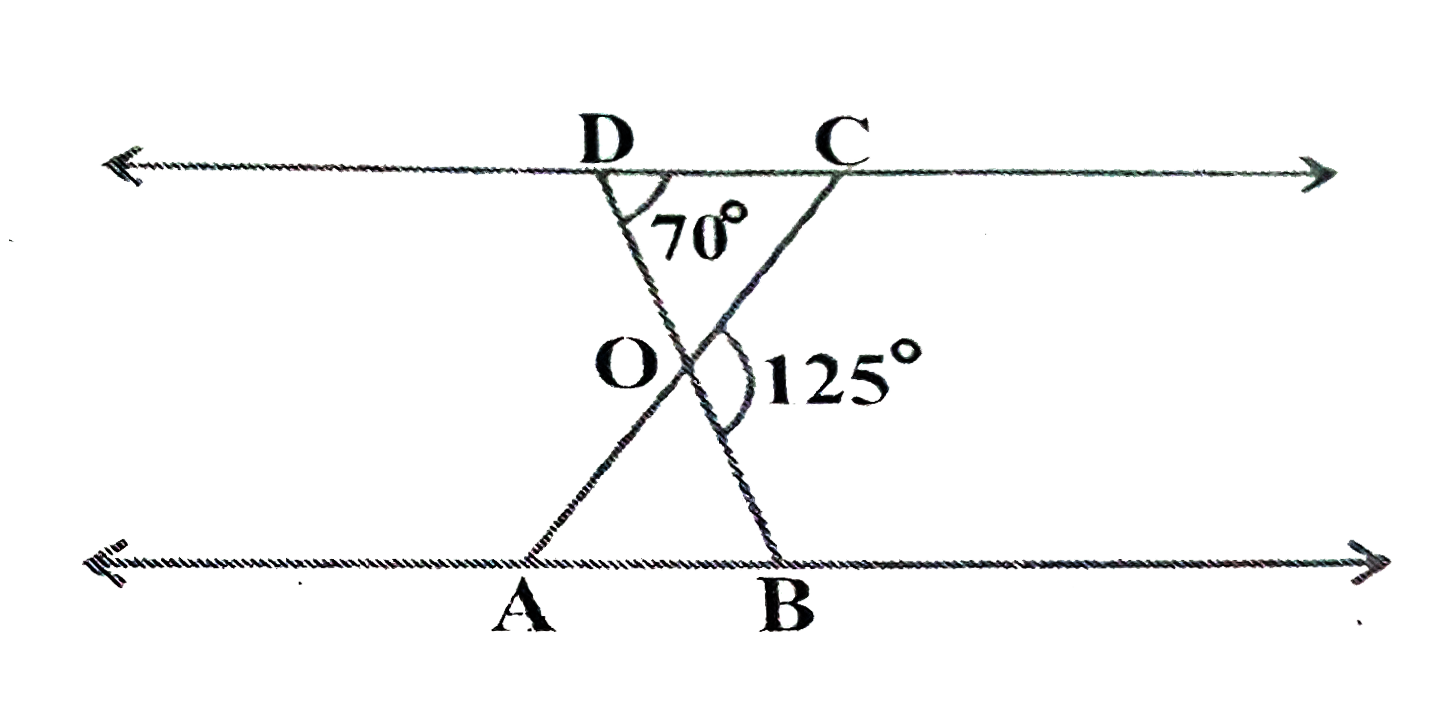
View Solution
In a quadrilateral $A B C D$ , given that $∠ A + ∠ D = 90 o$ . Prove that $A C^{2} + B D^{2} = A D^{2} + B C^{2}$ .
View Solution
In figure, ABC is triangle in which $∠ A B C = 90^{\circ}$ and $A D ⊥ C B$ produced. Prove that $A C^{2} = A B^{2} + B C^{2} - 2 B C . B D$ .

View Solution

Recommended Questions

Home
Ask Doubt
Profile