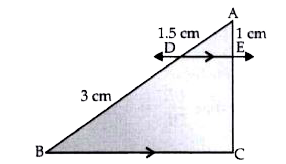
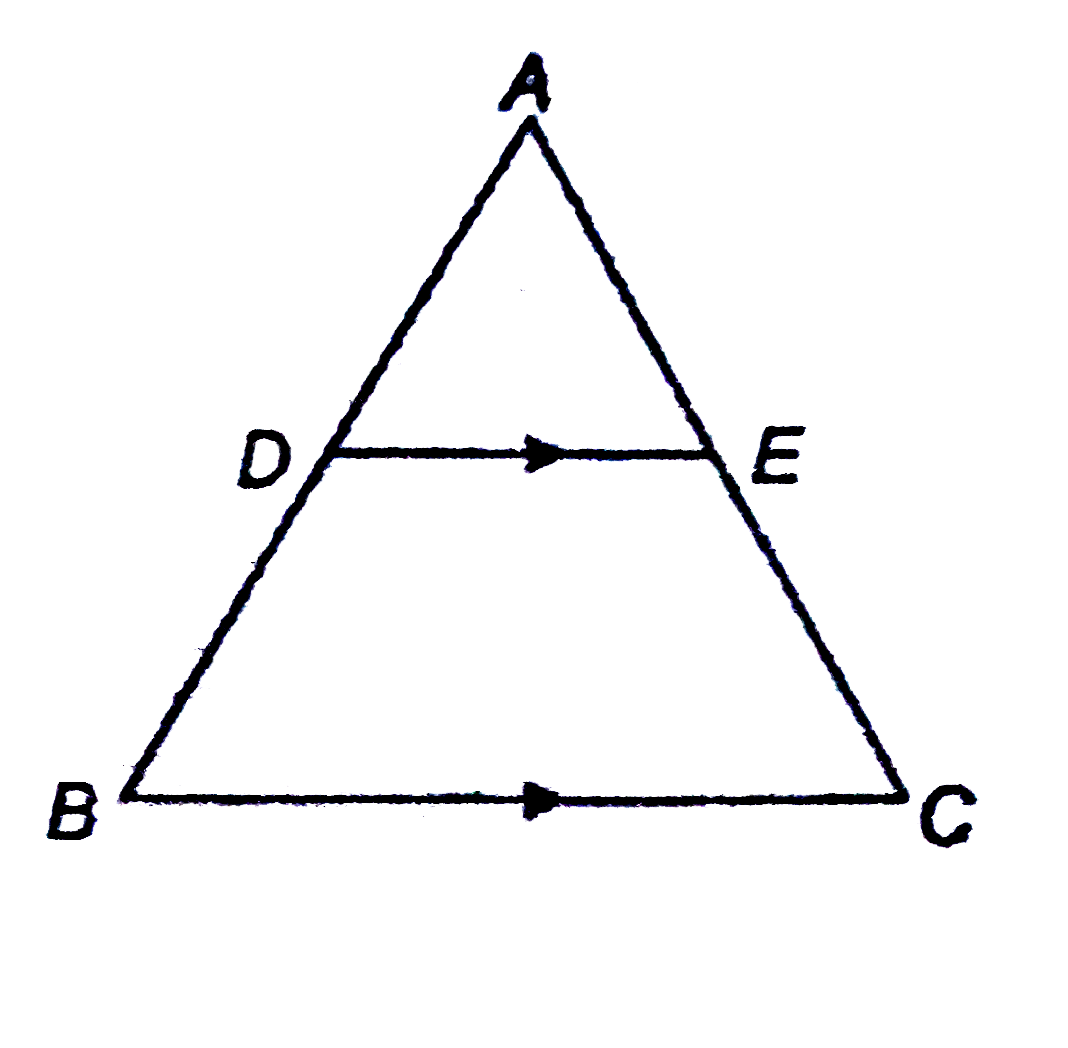
In Figure (i) and (ii), DE||BC. Find EC in (i) and AD in (ii).
Video Solution
Text Solution
(i) By basic proportionality theorem,
ADDB=AEEC
Putting the values,
1.53=1EC
1.5×EC=1×3
EC=1×31.5
EC=2cm
(ii) By basic proportionality theorem,
ADDB=AEEC
Putting the values,
AD7.2=1.85.4
AD×5.4=1.8×7.2
AD=1.8×7.25.4
AD=2.4cm
|
Similar Questions
Knowledge Check
In the figure : DE||BC then the value of EC is :
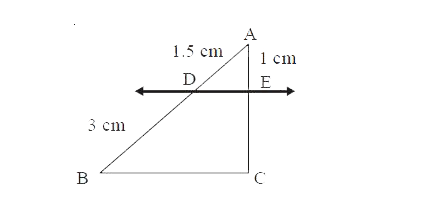 A1 cmB2 cmC1.5 cmD3 cm
A1 cmB2 cmC1.5 cmD3 cm
Find: (i) 6412 (ii) 3215 (iii) 12513
View SolutionIn the figure, DE∣∣BCandAE:EC=3:7. Find
View SolutionEvaluate
(i) 8!
(ii) 4!−3!
View SolutionIn the figure AB || CD, AD and BC intersect at o and O is mid-point of AD. Show that
(i) ΔAOB≅ΔDOCand(ii)OB=OC.
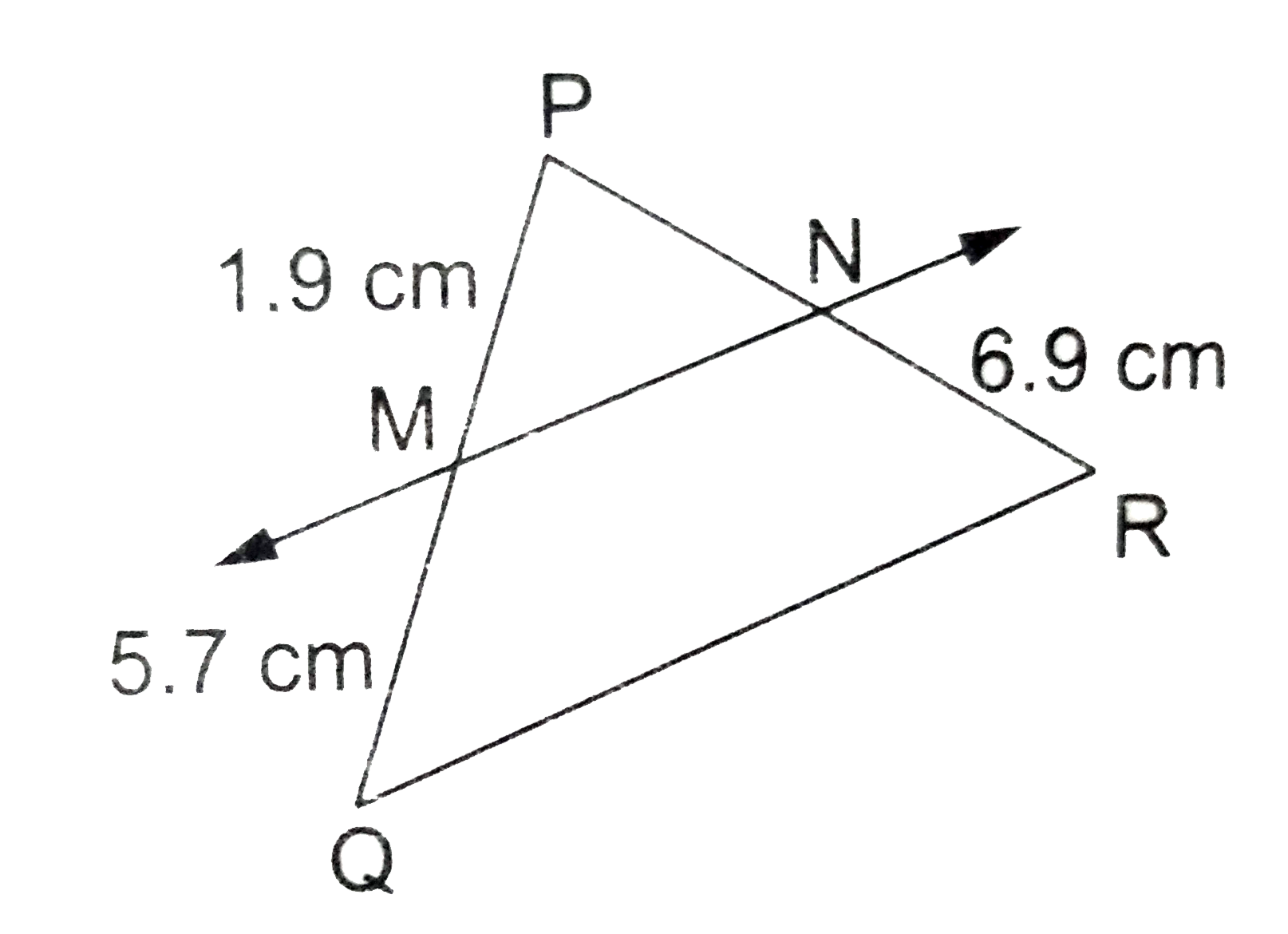
View SolutionIn the adjoining figure, MN∣∣QR.
Find (i) PN and (ii) PR.
View SolutionIn the adjoining figure DE||BE and D divides AB in the ratio 2:3 find.
(i) AEEC (ii) AEAC
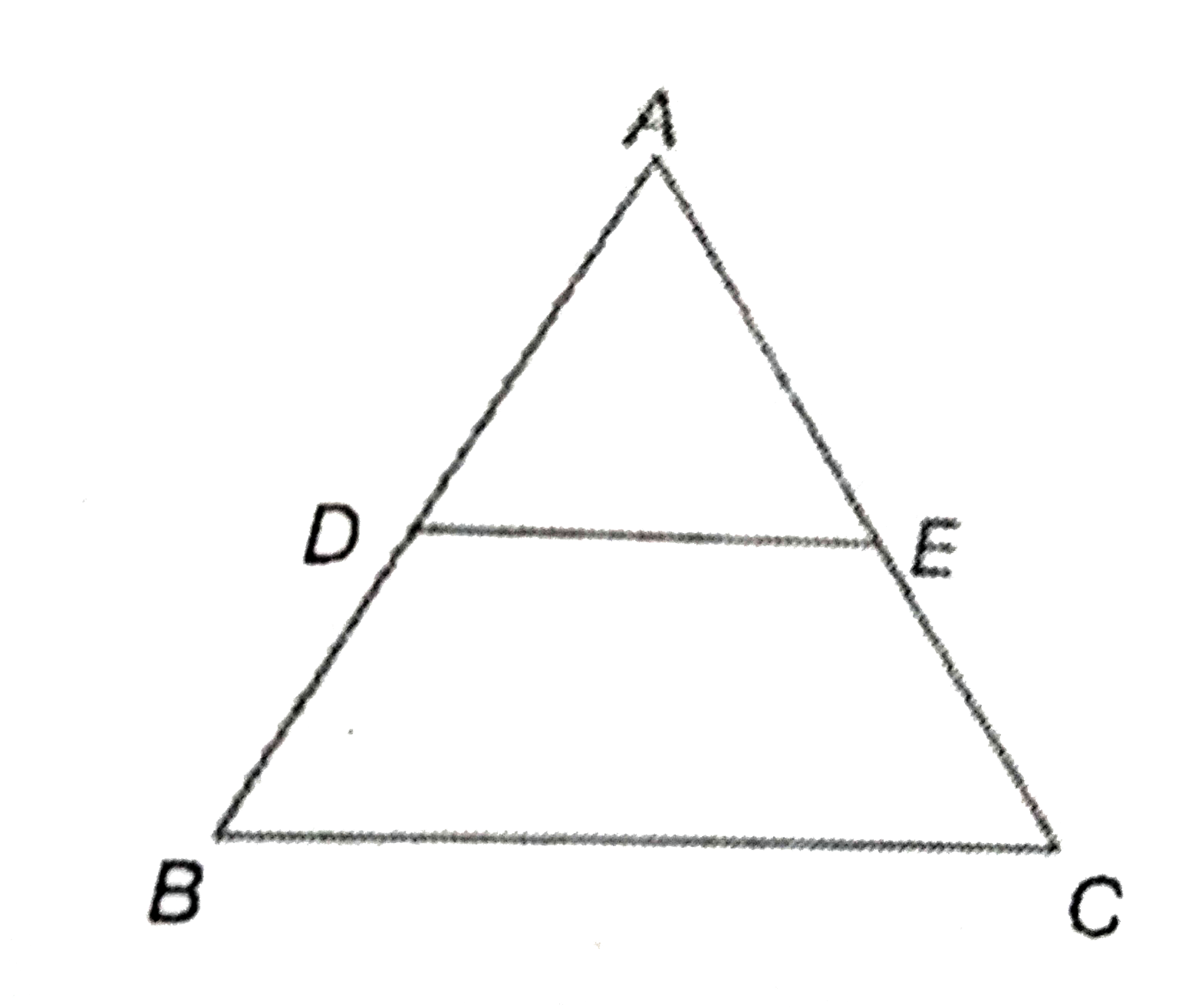
View SolutionIn the following figure, AD=DB and DE∣∣BC. Then AE=EC (True/ False)
View Solution