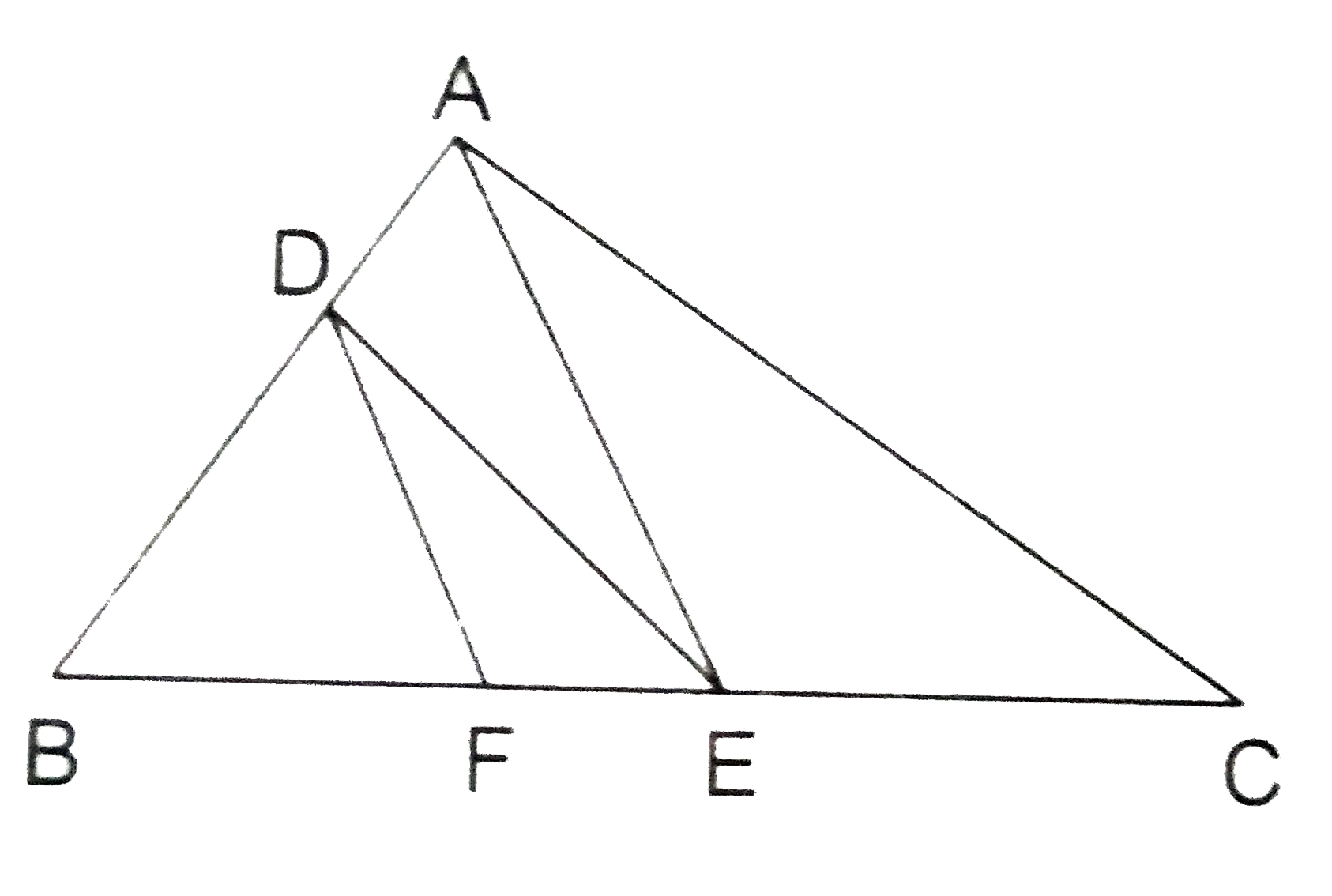
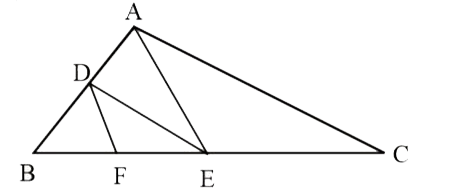
In figure, DE || AC and DF || AE. Prove that .
In ,
(given)
By basic proportionality theorem,
...(i)
Again In ,
(given)
By basic proportionality theorem,
...(ii)
Thus, form (i) and (ii),
Hence proved.
Similar Questions
Knowledge Check
In the figure below, DE || AC and DF || AE. Which of these is equal to BFFE ?
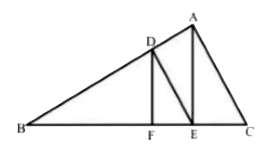 ADFAEBBEBCCBAACDFEEC
ADFAEBBEBCCBAACDFEEC
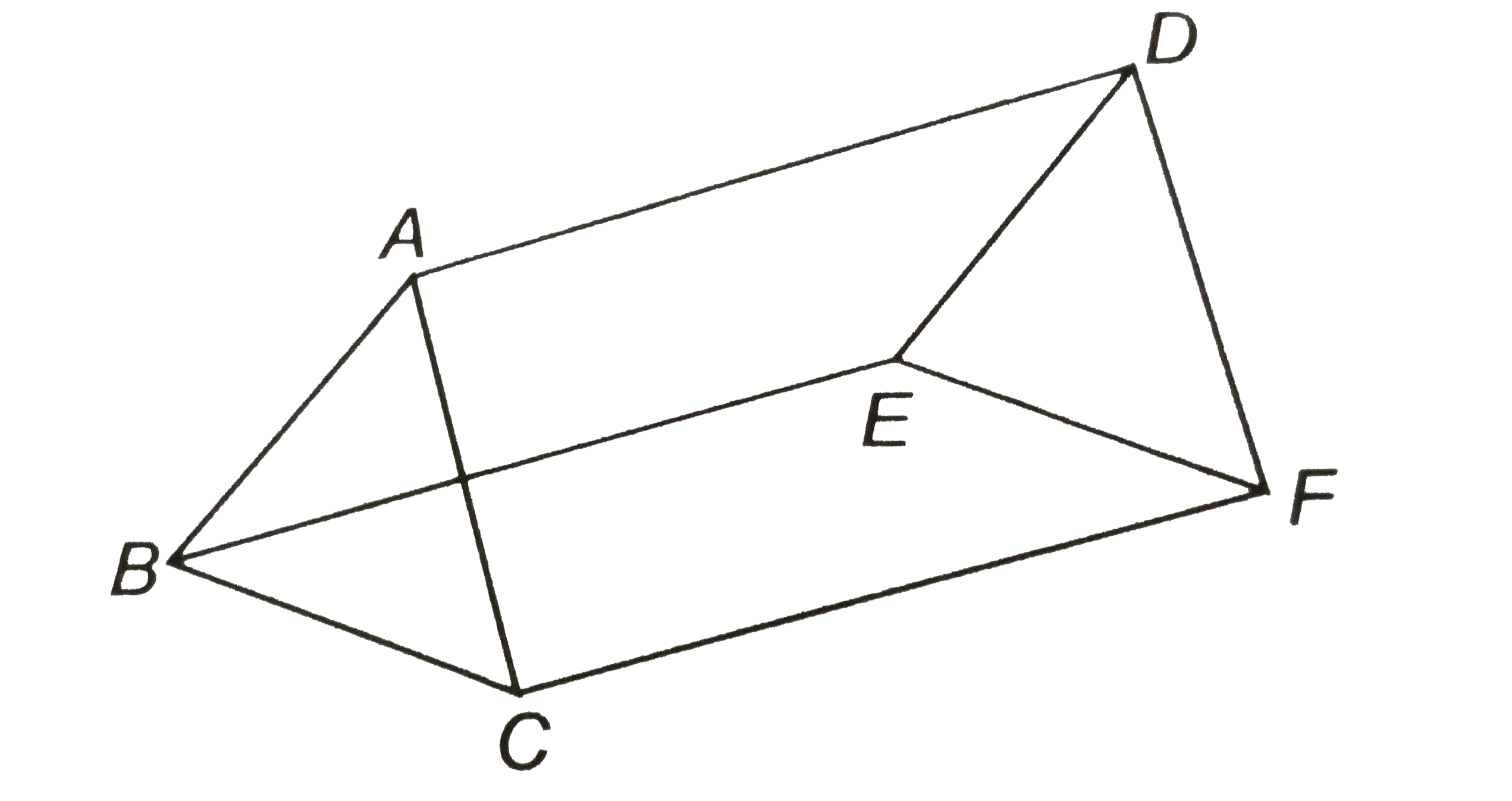
In figure, AB||DE, AB=DE, AC||DF and AC=DF. Prove that BC||EF and BC=EF.
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)= 2:5 (b) 4:25 (c) 4:15 (d) 8:125
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD
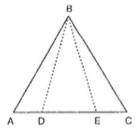
View SolutionIn Figure, AD is the median and DE∣∣AB . Prove that BE is the median.
View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
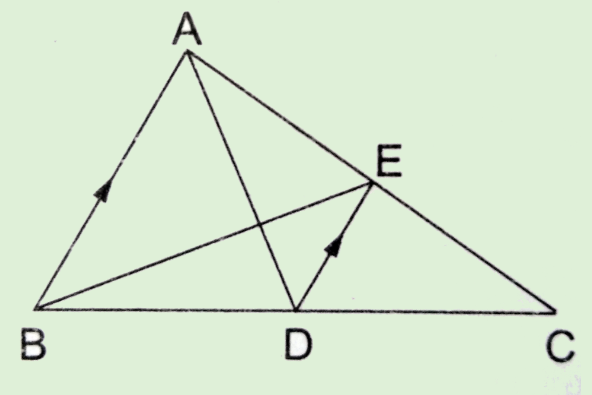
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14AC
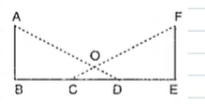
View SolutionIn Figure, it is given that AB=EF,BC=DE,AB⊥BD and FE⊥CE. Prove that ABD≅FEC.
View Solution