For a frequency distribution standard deviation is computed by
σ=Σf(x−¯x)Σf
σ=√Σf(x−¯x)2Σf
σ=√Σf(x−¯x)2Σf
σ=√Σ(x−¯x)Σf
The correct Answer is:C
To find the standard deviation for a frequency distribution, we can follow these steps:
Step 1: Understand the Components
- n: Total number of observations (sum of frequencies).
- fi: Frequency of each observation.
- xi: Each observation value.
- x̄: Mean of the distribution.
Step 2: Calculate the Mean (x̄)
The mean for a frequency distribution is calculated using the formula:
xˉ=∑(fi⋅xi)n
Where:
- ∑(fi⋅xi) is the sum of the product of frequencies and observations.
- n=∑fi is the total number of observations.
Step 3: Calculate the Variance (σ²)
The variance for a frequency distribution is given by:
σ2=∑fi(xi−xˉ)2n
This can also be expressed as:
σ2=∑fix2i−n⋅(xˉ)2n
Where:
- ∑fix2i is the sum of the squares of the observations multiplied by their frequencies.
Step 4: Calculate the Standard Deviation (σ)
The standard deviation is the square root of the variance:
σ=√σ2
Thus, substituting the variance formula, we get:
σ=√∑fi(xi−xˉ)2n
or
σ=√∑fix2i−n⋅(xˉ)2n
Conclusion
The correct formula to compute the standard deviation for a frequency distribution is:
σ=√∑fi(xi−xˉ)2n
- n: Total number of observations (sum of frequencies).
- fi: Frequency of each observation.
- xi: Each observation value.
- x̄: Mean of the distribution.
The mean for a frequency distribution is calculated using the formula:
xˉ=∑(fi⋅xi)n
Where:
- ∑(fi⋅xi) is the sum of the product of frequencies and observations.
- n=∑fi is the total number of observations.
The variance for a frequency distribution is given by:
σ2=∑fi(xi−xˉ)2n
This can also be expressed as:
σ2=∑fix2i−n⋅(xˉ)2n
Where:
- ∑fix2i is the sum of the squares of the observations multiplied by their frequencies.
The standard deviation is the square root of the variance:
σ=√σ2
Thus, substituting the variance formula, we get:
σ=√∑fi(xi−xˉ)2n
or
σ=√∑fix2i−n⋅(xˉ)2n
The correct formula to compute the standard deviation for a frequency distribution is:
σ=√∑fi(xi−xˉ)2n
Topper's Solved these Questions
- STATISTICSBook:FIITJEEChapter:STATISTICSExercise:Assertion -Reasoning Type MCQ Single Correct(Level II)
Explore 2 Videos
- STATISTICSBook:FIITJEEChapter:STATISTICSExercise:Comprehension Type
Explore 6 Videos
- STATISTICSBook:FIITJEEChapter:STATISTICSExercise:Assignment Problems (Objective) Level -I
Explore 20 Videos
- SET, RELATION & FUNCTIONBook:FIITJEEChapter:SET, RELATION & FUNCTIONExercise:Exercise 3
Explore 8 Videos
- STRAIGHT LINE Book:FIITJEEChapter:STRAIGHT LINE Exercise:NUMERICAL BASED
Explore 4 Videos
Similar Questions
Knowledge Check
For a frequency distribution 7th decile is computed by the formula
AD7=l+(n7−c))f×iBD7=l+(n10−c))f×iCD7=l+(7n10−c))f×iDD7=l+(10n7−c))f×iFor a frequency distribution the mean deviation about mean is computed by
AM.D. =∑d1∑fiBM.D.=∑fidi∑fiCM.D.=∑fi|di|∑fiDM.D.=∑fi∑fi|di|For a frequency distribution lower quartile is computed by
AQ1=l+N4−Cf×iBQ1=l+(N2)−Cf×iCQ1=l+(3N4−C))f×iDQ1=l+(N−C)f×i
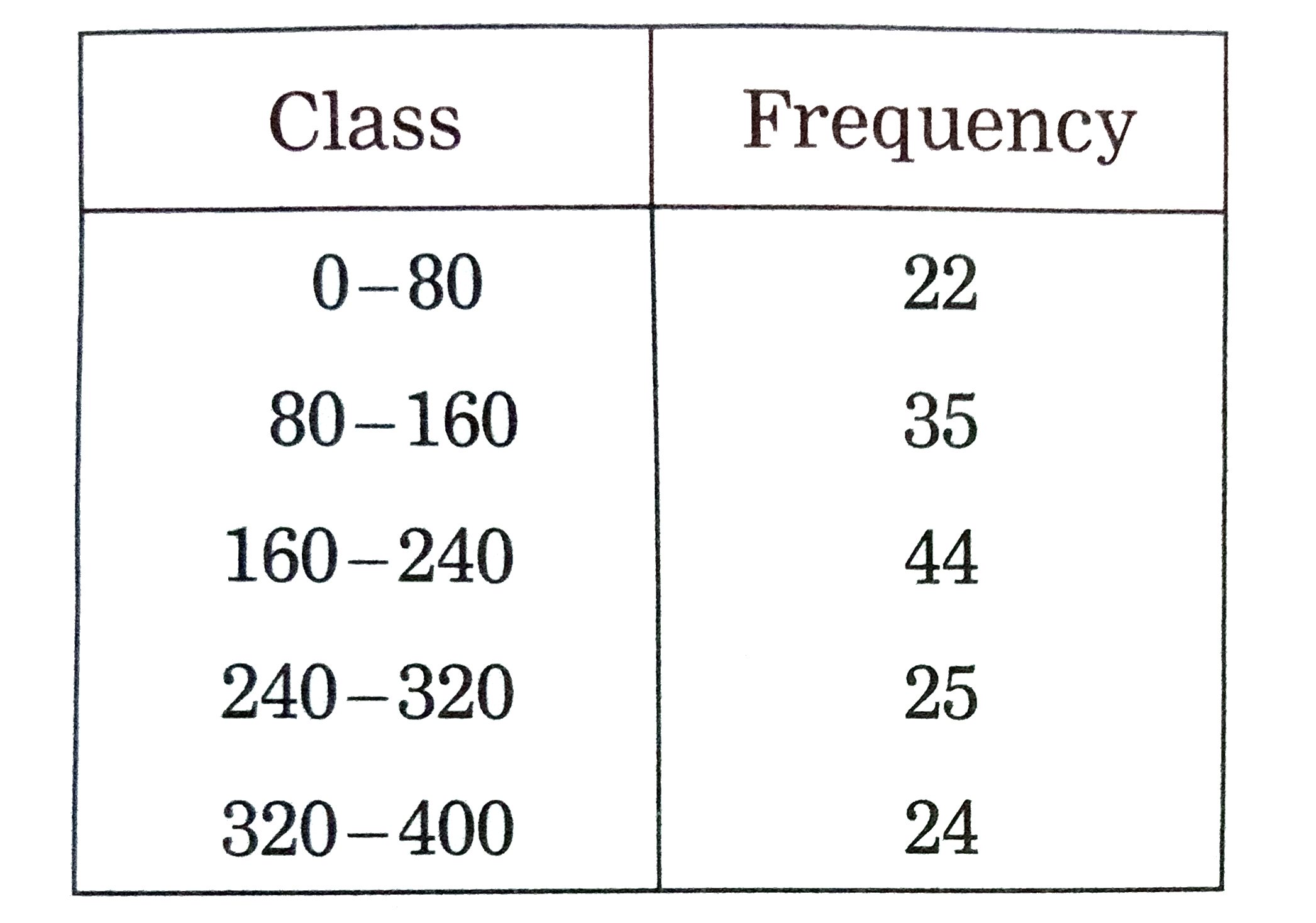
Calculate the mean of the following frequency distribution : (Use step deviation method .)
View SolutionIf the mean of a binomial distribution is 20 and its standard deviation is 4, find p .
View SolutionThe mean of a distribution is 13 and the standard deviation is 7. What is the value of the coefficient variation?
View SolutionThe mean of a distribution is 15 and the standard deviation is 5. What is the value of the coefficient variation?
View SolutionThe mean of a binomial distribution is 15 and standard deviation is 5, then which one of the following is correct ?
View Solution

