Calculate the mean deviation (about mean) and standard deviation of the following data:
25,50,48,70,45,33,51,31,60
The correct Answer is:M.D. (about mean)=11.64 S.D.=13.71
To solve the problem of calculating the mean deviation (about the mean) and standard deviation for the given data set: 25, 50, 48, 70, 45, 33, 51, 31, 60, we will follow these steps:
Step 1: Calculate the Mean
First, we need to find the mean (average) of the data set.
Mean(¯x)=∑xin
Where n is the number of observations.
∑xi=25+50+48+70+45+33+51+31+60=413
n=9
¯x=4139≈45.89
Step 2: Calculate the Mean Deviation
Next, we calculate the mean deviation about the mean. The mean deviation is given by:
Mean Deviation=∑|xi−¯x|n
We will calculate |xi−¯x| for each observation:
- |25−45.89|=20.89
- |50−45.89|=4.11
- |48−45.89|=2.11
- |70−45.89|=24.11
- |45−45.89|=0.89
- |33−45.89|=12.89
- |51−45.89|=5.11
- |31−45.89|=14.89
- |60−45.89|=14.11
Now, we sum these absolute deviations:
∑|xi−¯x|=20.89+4.11+2.11+24.11+0.89+12.89+5.11+14.89+14.11=99.11
Now, we can calculate the mean deviation:
Mean Deviation=99.119≈11.01
Step 3: Calculate the Standard Deviation
The standard deviation is calculated using the formula:
Standard Deviation=√∑(xi−¯x)2n
We first calculate (xi−¯x)2 for each observation:
- (25−45.89)2=436.5921
- (50−45.89)2=16.9921
- (48−45.89)2=4.4521
- (70−45.89)2=580.5921
- (45−45.89)2=0.7921
- (33−45.89)2=168.7921
- (51−45.89)2=26.5921
- (31−45.89)2=219.5921
- (60−45.89)2=197.5921
Now, we sum these squared deviations:
∑(xi−¯x)2=436.5921+16.9921+4.4521+580.5921+0.7921+168.7921+26.5921+219.5921+197.5921=1652.9
Now we can calculate the standard deviation:
Standard Deviation=√1652.99≈√183.65≈13.55
Final Results
- Mean Deviation: ≈11.01
- Standard Deviation: ≈13.55
---
First, we need to find the mean (average) of the data set.
Next, we calculate the mean deviation about the mean. The mean deviation is given by:
- |50−45.89|=4.11
- |48−45.89|=2.11
- |70−45.89|=24.11
- |45−45.89|=0.89
- |33−45.89|=12.89
- |51−45.89|=5.11
- |31−45.89|=14.89
- |60−45.89|=14.11
The standard deviation is calculated using the formula:
- (50−45.89)2=16.9921
- (48−45.89)2=4.4521
- (70−45.89)2=580.5921
- (45−45.89)2=0.7921
- (33−45.89)2=168.7921
- (51−45.89)2=26.5921
- (31−45.89)2=219.5921
- (60−45.89)2=197.5921
- Mean Deviation: ≈11.01
- Standard Deviation: ≈13.55
Topper's Solved these Questions
- STATISTICSBook:FIITJEEChapter:STATISTICSExercise:Exercise 2
Explore 4 Videos
- STATISTICSBook:FIITJEEChapter:STATISTICSExercise:Exercise 3
Explore 2 Videos
- STATISTICSBook:FIITJEEChapter:STATISTICSExercise:Solved Problems(Objective)
Explore 24 Videos
- SET, RELATION & FUNCTIONBook:FIITJEEChapter:SET, RELATION & FUNCTIONExercise:Exercise 3
Explore 8 Videos
- STRAIGHT LINE Book:FIITJEEChapter:STRAIGHT LINE Exercise:NUMERICAL BASED
Explore 4 Videos
Similar Questions
Calculate mean and standard deviation from the following data:
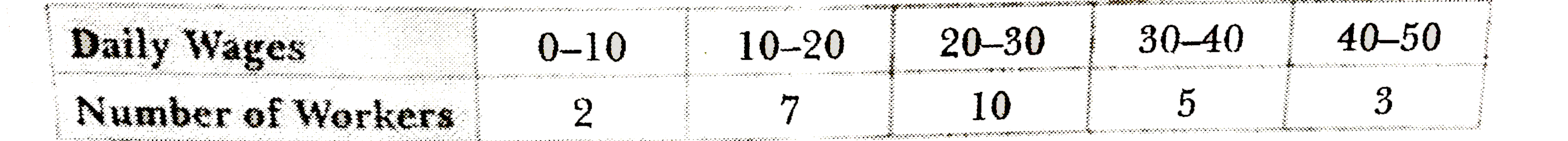
View SolutionCalculate the Mean Deviation about Mean and Standard Deviation for the following distribution:
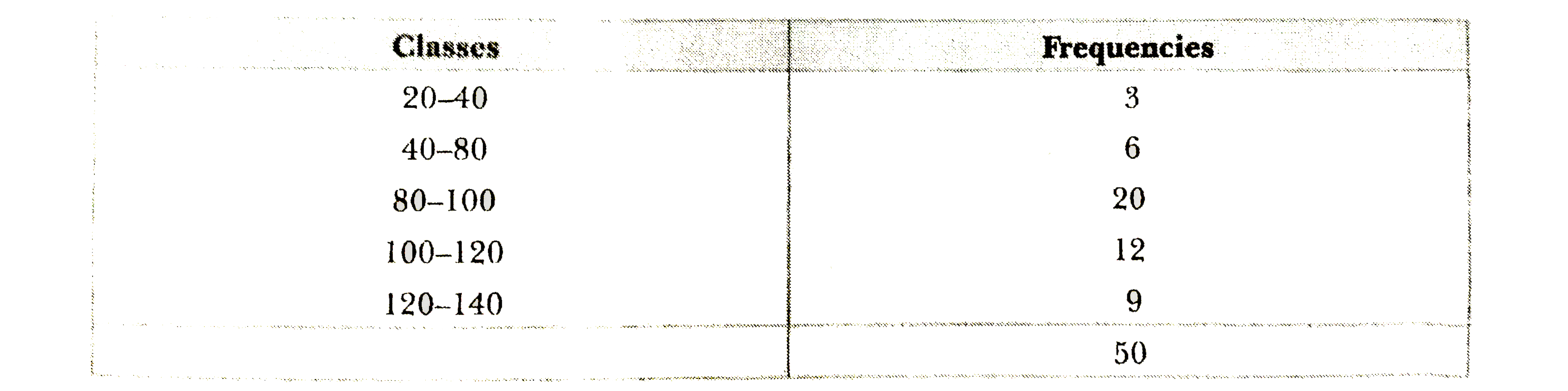
View SolutionCalculate the standard deviation from the following data:
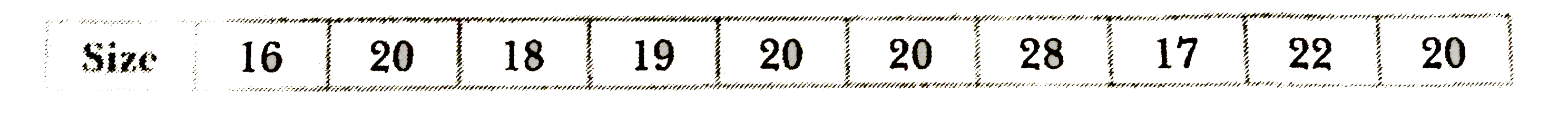
View SolutionCalculate standard deviation from the following data:

View SolutionFind the mean , mean deviation about the mean , variance and standard deviation for the following data
4,15,14,12,6,8,11
View SolutionFind the mean , mean deviation about the mean , variance and standard deviation for the following data

View SolutionCalculate the mean deviation about median for the following data :
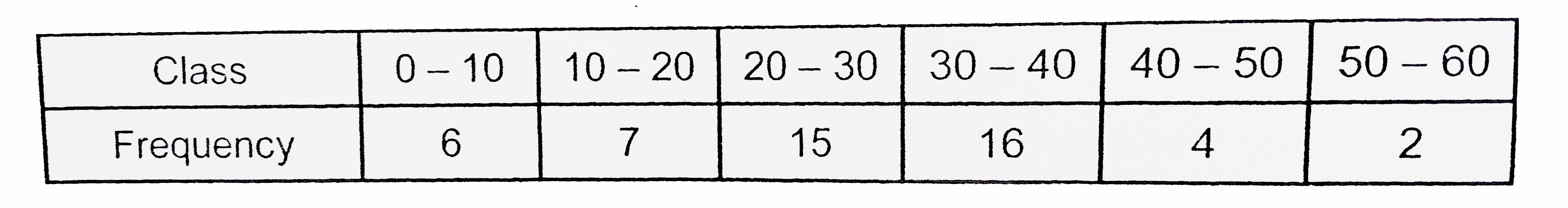
View SolutionCalcualte the mean deviation about mean for the following data:

View SolutionCalculate the mean deviation about median for the following data :
View SolutionCalculate the mean deviation about median for the following data:

View Solution