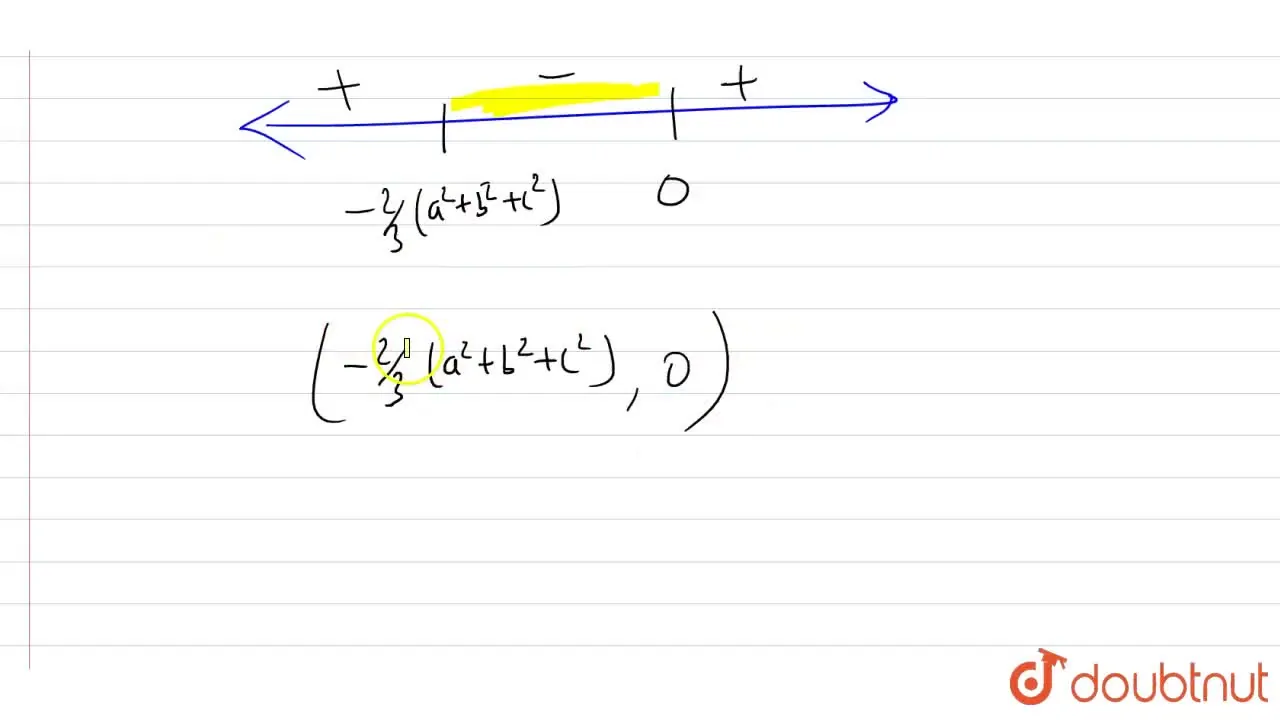if a,b,c are real then find the intervial in which f(x)=∣∣ ∣ ∣∣x+a2abacabx+b2bcacbcx+c2∣∣ ∣ ∣∣ is decreasing.
The correct Answer is:(−23(a2+b2+c2),0)
Step by step video, text & image solution for if a,b,c are real then find the intervial in which f(x)=|{:(x+a^2,ab,ac),(ab,x+b^2,bc),(ac,bc,x+c^2):}| is decreasing. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - FIITJEECHAPTER - DETERMINANTEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I53videos
DETERMINANT
- BOOK - FIITJEECHAPTER - DETERMINANTEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level -II19videos
DETERMINANT
- BOOK - FIITJEECHAPTER - DETERMINANTEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) (LEVEL-I) Fill in the blanks4videos
DETERMINANT
- BOOK - FIITJEECHAPTER - DEFINITE INTEGRAL EXERCISE - NUMERICAL BASED3videos
DEFINITE INTEGRAL
- BOOK - FIITJEECHAPTER - ELLIPSEEXERCISE - NUMERICAL BASED4videos
ELLIPSE
Similar Questions
If a, b, c are real numbers, then find the intervals in which :
f(x)=∣∣ ∣ ∣∣x+a2abacabx+b2bcacbcx+c2∣∣ ∣ ∣∣ is strictly increasing or decreasing.View SolutionWhat is ∣∣ ∣ ∣∣−a2abacab−b2bcacbc−c2∣∣ ∣ ∣∣ equal to ?
View SolutionIf a,b,c be real , then determine the interval of monotonicity of the function
f(x)=∣∣ ∣ ∣∣x+a2abacabx+b2bcacbcx+c2∣∣ ∣ ∣∣View SolutionIf ∣∣ ∣ ∣∣−a2abacab−b2bcacbc−c2∣∣ ∣ ∣∣=ka2b2c2 , then k =
View SolutionWhat is the value of ∣∣ ∣ ∣∣−a2abacab−b2bcacbc−c2∣∣ ∣ ∣∣ ?
View SolutionThe determinant
Δ=∣∣ ∣ ∣∣a2+xabacabb2+xbcacbcc2+x∣∣ ∣ ∣∣ is divisible byView Solution∣∣ ∣ ∣∣x2+a2abacabx2+b2bcacbcx2+c2∣∣ ∣ ∣∣=
View SolutionIf a,b,c be real, then f(x)=∣∣ ∣ ∣∣x+a2abababx+b2bcacbcx+c2∣∣ ∣ ∣∣ is decreasing on
View SolutionIf ∣∣ ∣ ∣∣a2+1abacabb2+1bcacbcc2+1∣∣ ∣ ∣∣=1 , where a,b,c are real , then
View SolutionThe determinant Δ=∣∣ ∣ ∣∣a2+x2abacabb2+x2bcacbcc2+x2∣∣ ∣ ∣∣ is divisible by
View Solution