Two friends visit a restaurant randomly during 5 pm to 6 pm . Among

Class 12 MATHS PROBABILITY

Topper's Solved these Questions

PROBABILITYBOOK - FIITJEECHAPTER - PROBABILITYEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I
54 Videos
PROBABILITYBOOK - FIITJEECHAPTER - PROBABILITYEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II
20 Videos
PROBABILITYBOOK - FIITJEECHAPTER - PROBABILITYEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Fill in the blanks (Q-11- Q-15):
5 Videos
PERMUTATIONS & COMBINATIONSBOOK - FIITJEECHAPTER - PERMUTATIONS & COMBINATIONSEXERCISE - NUMERICAL BASED
3 Videos
PROGRESSION & SERIES BOOK - FIITJEECHAPTER - PROGRESSION & SERIES EXERCISE - NUMERICAL BASED
3 Videos

Knowledge Check

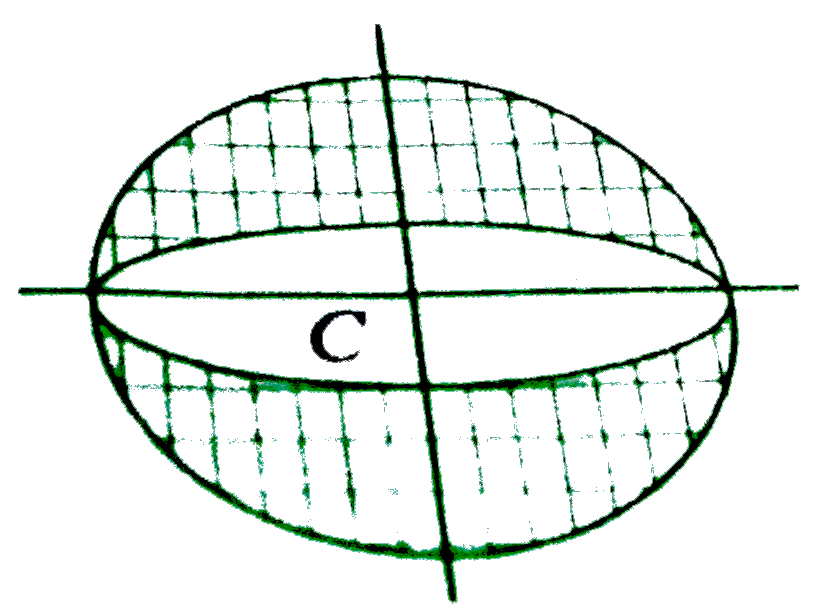
There are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity $2 \sqrt{2} / 3$ is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
$1 - \frac{b^{2}}{a^{2}} = \frac{8}{9} or \frac{b^{2}}{a^{2}} = \frac{1}{9}$
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
$p = \frac{Area of shaded region}{Area of circle}$
$= \frac{π a^{2} - π a b}{π a^{2}} = 1 - \frac{b}{a} = 1 - \frac{1}{3} = \frac{2}{3}$
Now, answer the following questions.

Two persons A and B agree to meet at a place between 5 and 6 pm. The first one to arrive waits for 20 min and then leave. If the time of their arrival be independant and at random, then the probability that A and B meet is
A $1 / 3$
B $1 / 3$
C $2 / 3$
D $5 / 9$
Two persons ordered tea in a restaurant and waited for a friend to arrive. The first person mixed hot tea and cold milk in the cup and wated for the fried and the second mixed hot tea and hot milk in the cup after the arrival of the friend. Milk in the cup after the arrival of the friend. If the temperature of the two cups of tea are $T_{1} and T_{2}$ respectively, then.
A $T_{1} < T_{2}$
B $T_{1} = T_{2}$
C $T_{1} > T_{2}$
D $T_{1} \geq T_{2}$
Two numbers are selected randomly from the set $S = {1, 2, 3, 4, 5, 6}$ without replacement. The probability that minimum of the two numbers is less than 4, is
A $1 / 15$
B $14 / 15$
C $1 / 5$
D $4 / 5$

Two friends visit a restaurant randomly during 5 pm to 6 pm . Among the two, whoever comes first waits for 15 min and then leaves. The probability that they meet is :

The correct Answer is: $\frac{7}{16}$

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two numbers are selected randomly from the set $S = {1, 2, 3, 4, 5, 6}$ without replacement. The probability that minimum of the two numbers is less than 4, is

FIITJEE-PROBABILITY-ASSIGNMENT PROBLEMS (SUBJECTIVE) Level -II

Two friends visit a restaurant randomly during 5 pm to 6 pm . Among the two, whoever comes first waits for 15 min and then leaves. The probability that they meet is :

The correct Answer is:716

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two numbers are selected randomly from the set S={1,2,3,4,5,6} without replacement. The probability that minimum of the two numbers is less than 4, is

FIITJEE-PROBABILITY-ASSIGNMENT PROBLEMS (SUBJECTIVE) Level -II

The correct Answer is: $\frac{7}{16}$

Two numbers are selected randomly from the set $S = {1, 2, 3, 4, 5, 6}$ without replacement. The probability that minimum of the two numbers is less than 4, is