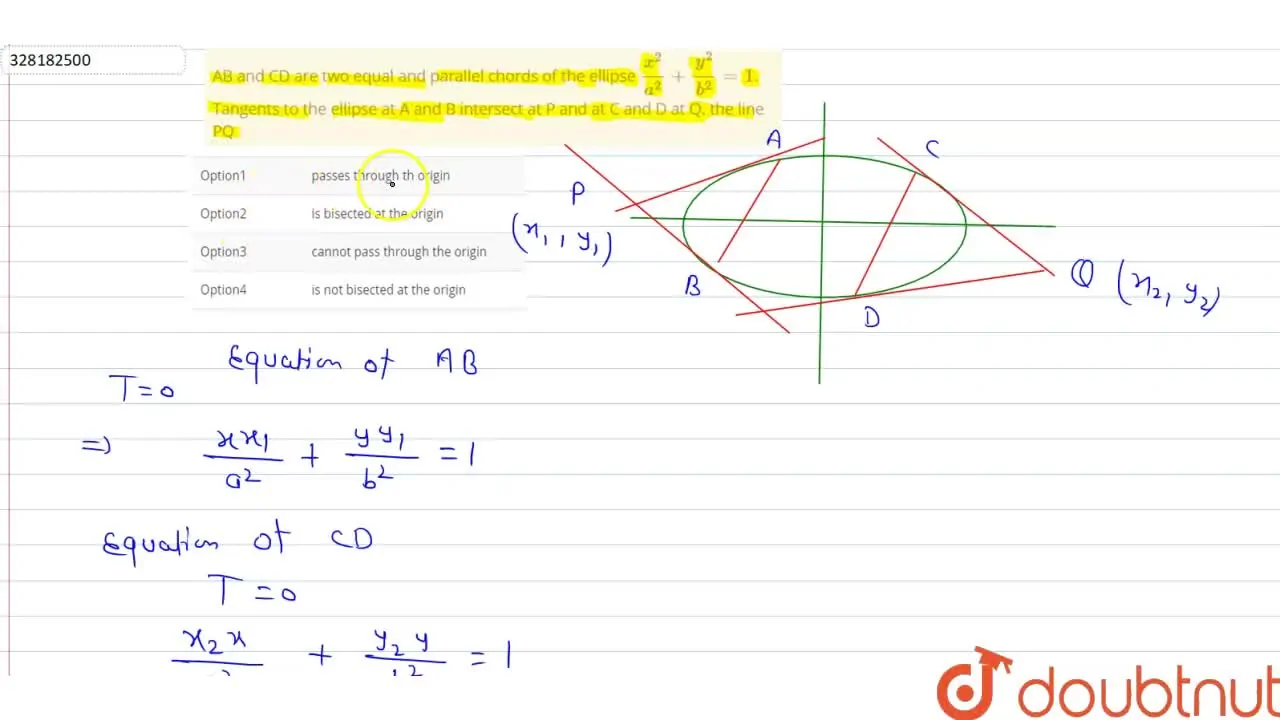
AB and CD are two equal and parallel chords of the ellipse . Tangents to the ellipse at A and B intersect at P and at C and D at Q. the line PQ
passes through th origin
is bisected at the origin
cannot pass through the origin
is not bisected at the origin
Step by step video & image solution for AB and CD are two equal and parallel chords of the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1. Tangents to the ellipse at A and B intersect at P and at C and D at Q. the line PQ by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - FIITJEECHAPTER - ELLIPSEEXERCISE - EXERCISE 15videos
ELLIPSE
- BOOK - FIITJEECHAPTER - ELLIPSEEXERCISE - EXERCISE 29videos
ELLIPSE
- BOOK - FIITJEECHAPTER - ELLIPSEEXERCISE - SOLVED PROBLEMS (SUBJECTIVE)11videos
ELLIPSE
- BOOK - FIITJEECHAPTER - DETERMINANTEXERCISE - NUMERICAL BASED3videos
DETERMINANT
- BOOK - FIITJEECHAPTER - FUNCTIONEXERCISE - NUMERICAL BASED3videos
FUNCTION
Similar Questions
AB and CD are two equal and parallel chords of the ellipse x2a2+y2b2=1. Tangents to the ellipse at A and B intersect at P and tangents at C and D at Q. The line PQ
View SolutionThe line y=mx+c is a normal to the ellipse x2a2+y2b2=1, if c
View SolutionThe ellipse x2a2+y2b2=1 and the straight line y=mx+c intersect in real points only if:
View SolutionFind the maximum length of chord of the ellipse x2a2+y2b2=1 then find the locus of midpoint of PQ
View SolutionIf y=mx+c is a tangent to the ellipse x2a2+y2b2=1 then the point of contact is
View SolutionIf the focal chord of the ellipse x2a2+y2b2=1, is normal at (acosθ,bsinθ) then eccentricity of the ellipse is
View SolutionIf p and q are the segments of a focal chord of an ellipse b2x2+a2y2=a2b2 then
View SolutionIf the line containing a focal chord of the ellipse x2a2+y2b2=1 intersects the auxiliary circle in QandQ1 then SQ.SQ1=
View SolutionLet a tangent at a point P to the ellipse x2a2+y2b2=1 meets directrix at Q and S be the correspondsfocus then ∠PSQ
View SolutionFind the eccentric angle of the point P on the ellipse x2a2+y2b2=1 tangent at which, is equally inclined to the axes.
View Solution