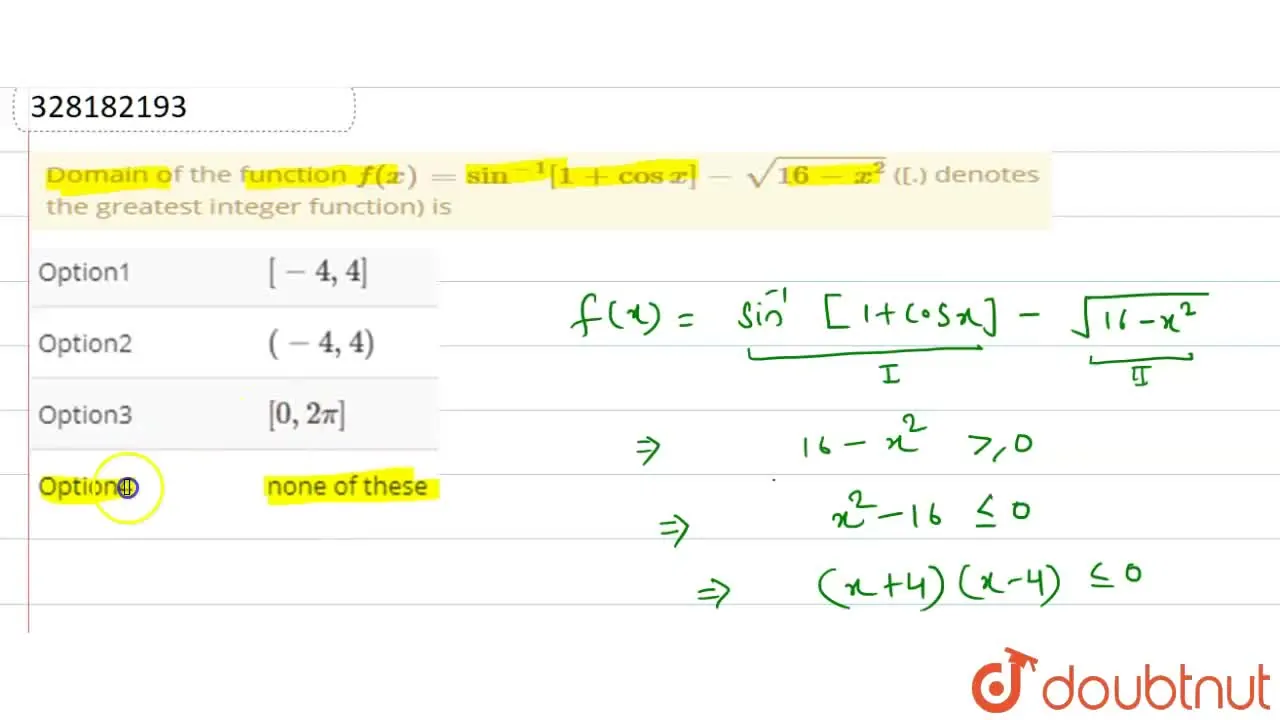
Domain of the function f(x)=sin−1[1+cosx]−√16−x2 ([.) denotes the greatest integer function) is

A

[−4,4]

B

(−4,4)

C

[0,2π]

D

none of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Generated By DoubtnutGPT

The correct Answer is:D

To find the domain of the function f(x)=sin−1(1+cosx)−√16−x2, we need to analyze both components of the function separately.

Step 1: Analyze the square root component
The first component we analyze is −√16−x2. For the square root to be defined, the expression inside the square root must be non-negative:

16−x2≥0

Rearranging gives:

x2≤16

Taking the square root of both sides, we find:

−4≤x≤4

Thus, the domain from this part is:

x∈(−4,4)

Step 2: Analyze the sine inverse component
Next, we analyze the component sin−1(1+cosx). The sine inverse function is defined for inputs in the range (−1,1). Therefore, we need:

−1≤1+cosx≤1

Breaking this down into two inequalities:

1. First Inequality:
−1≤1+cosx⟹−2≤cosx
Since the cosine function has a range of (−1,1), this inequality is always satisfied for all x.

2. Second Inequality:
1+cosx≤1⟹cosx≤0
This means that x must be in the intervals where the cosine function is non-positive. The cosine function is non-positive in the intervals:

x∈(π2+2nπ,3π2+2nπ),n∈Z

Step 3: Combine the conditions
Now we need to find the intersection of the two conditions:

1. From the square root condition, we have x∈(−4,4).
2. From the sine inverse condition, we have x values where cosx≤0.

The critical points in the interval (−4,4) where cosx=0 are x=π2 and x=3π2.

Calculating these values:
- π2≈1.57
- 3π2≈4.71

Thus, within the interval (−4,4), the relevant interval for x where cosx≤0 is:

x∈(π2,4)

Step 4: Exclude points where the function is undefined
Next, we check for points where the function is undefined. The term sin−1(1+cosx) becomes undefined when 1+cosx>1, which occurs when cosx=1. This happens at x=2nπ.

In the interval (−4,4), the only point to exclude is x=0 (since 2nπ=0 when n=0).

Final Domain
Thus, the domain of the function f(x) is:

x∈(π2,4)∖{0}

Summary
The domain of the function is:

(π2,4) excluding 0

Updated on:18/9/2024
|
Class 12MATHSFUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If f(x)=[sin2x] ([.] denotes the greatest integer function), then

    Af is everywhere continuous
    Bf is everywhere differerntiable
    Cf is a constant function
    Dnone of these

  • Domain of f(x)=sin−1[2−4x2]([.] denotes the greatest integer function) is

    A[-1,1]
    B(-2,2)
    C[−√32,0]∪[0.√32]
    DNone of the above

  • The domain of the function f(x)=1√[x]2−[x]−20 is (where, [.] represents the greatest integer function)

    A(−∞,−4)∪[6,∞)
    B(−∞,4]∪[6,∞)
    C(−∞,4)∪(6,∞)
    DNone of these