A sphere is moving at some instant with horizontal velocity v0 in right and angular velocity ω in anti clockwise sense. If |v0|=|ωR|, the instantaneous centre of rotation is
at the bottom of the sphere
at the top of the sphere
at the centre of the sphere
anywhere inside the sphere
The correct Answer is:B
To find the instantaneous center of rotation for a sphere moving with a horizontal velocity v0 and an angular velocity ω in an anti-clockwise sense, we can follow these steps:
1. Understanding the Problem:
- We have a sphere moving horizontally to the right with a velocity v0.
- The sphere is also rotating anti-clockwise with an angular velocity ω.
- We are given that |v0|=|ωR|, where R is the radius of the sphere.
2. Defining Instantaneous Center of Rotation:
- The instantaneous center of rotation is the point on the object that has zero velocity at that instant. This point is crucial for analyzing the motion of the sphere.
3. Analyzing Velocities:
- The point at the bottom of the sphere (point P) will have a velocity due to both the translational motion v0 and the rotational motion ωR.
- The translational velocity v0 acts to the right.
- The rotational velocity at point P (which is at the bottom of the sphere) acts to the left and is equal to ωR.
4. Setting Up the Equation:
- Since we know that |v0|=|ωR|, we can express the velocities:
- Velocity at point P due to translation = v0 (to the right)
- Velocity at point P due to rotation = −ωR (to the left)
- Therefore, we can write:
vP=v0−ωR
5. Finding the Instantaneous Center:
- For the instantaneous center of rotation, we set the total velocity at point P to zero:
v0−ωR=0
- Since |v0|=|ωR|, we find that the velocity at point P is indeed zero.
6. Locating the Instantaneous Center:
- The instantaneous center of rotation lies directly below the center of the sphere at a distance equal to the radius R from the center of the sphere. This point is on the line of action of the velocity v0 and is located on the surface of the sphere.
Conclusion:
Thus, the instantaneous center of rotation is located at the point on the ground directly below the center of the sphere.
- We have a sphere moving horizontally to the right with a velocity v0.
- The sphere is also rotating anti-clockwise with an angular velocity ω.
- We are given that |v0|=|ωR|, where R is the radius of the sphere.
- The instantaneous center of rotation is the point on the object that has zero velocity at that instant. This point is crucial for analyzing the motion of the sphere.
- The point at the bottom of the sphere (point P) will have a velocity due to both the translational motion v0 and the rotational motion ωR.
- The translational velocity v0 acts to the right.
- The rotational velocity at point P (which is at the bottom of the sphere) acts to the left and is equal to ωR.
- Since we know that |v0|=|ωR|, we can express the velocities:
- Velocity at point P due to translation = v0 (to the right)
- Velocity at point P due to rotation = −ωR (to the left)
- Therefore, we can write:
vP=v0−ωR
- For the instantaneous center of rotation, we set the total velocity at point P to zero:
v0−ωR=0
- Since |v0|=|ωR|, we find that the velocity at point P is indeed zero.
- The instantaneous center of rotation lies directly below the center of the sphere at a distance equal to the radius R from the center of the sphere. This point is on the line of action of the velocity v0 and is located on the surface of the sphere.
Thus, the instantaneous center of rotation is located at the point on the ground directly below the center of the sphere.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - II
16 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - COMPREHENSION - III
1 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III
15 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type
6 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
Similar Questions
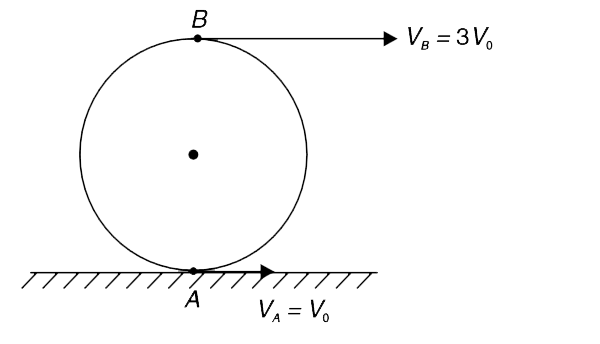
(i) A solid sphere of radius R is released on a rough horizontal surface with its top point having thrice the velocity of its bottom point A (VA=V0) as shown in figure. Calculate the linear velocity of the centre of the sphere when it starts pure rolling.
(ii) Solid sphere of radius R is placed on a rough horizontal surface with its centre having velocity V0 towards right and its angular velocity being ω0 (in anticlockwise sense). Find the required relationship between V0 and ω0 so that -
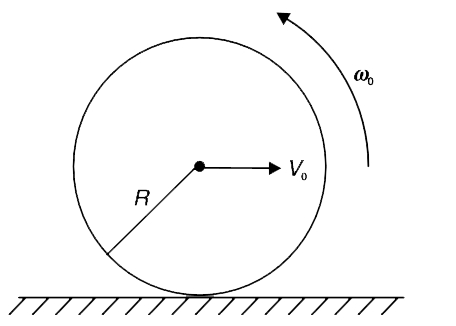
(a) the slipping ceases before the sphere loses all its linear momentum.
(b) the sphere comes to a permanent rest after some time.
(c) the velocity of centre becomes zero before the spinning ceases.
View SolutionA uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.

Disc will certainly come back to its intial position if
View Solution
Knowledge Check
Relation between Linear velocity (v) and Angular velocity (ω)
Av=rωBω=vωCr=vωDv=ωrA sphere is moving towards the positive x-axis with a velocity vc and rotates clockwise with angular speed ω shown in Fig. such that vc>ωR. The instantaneous axis of rotation will be
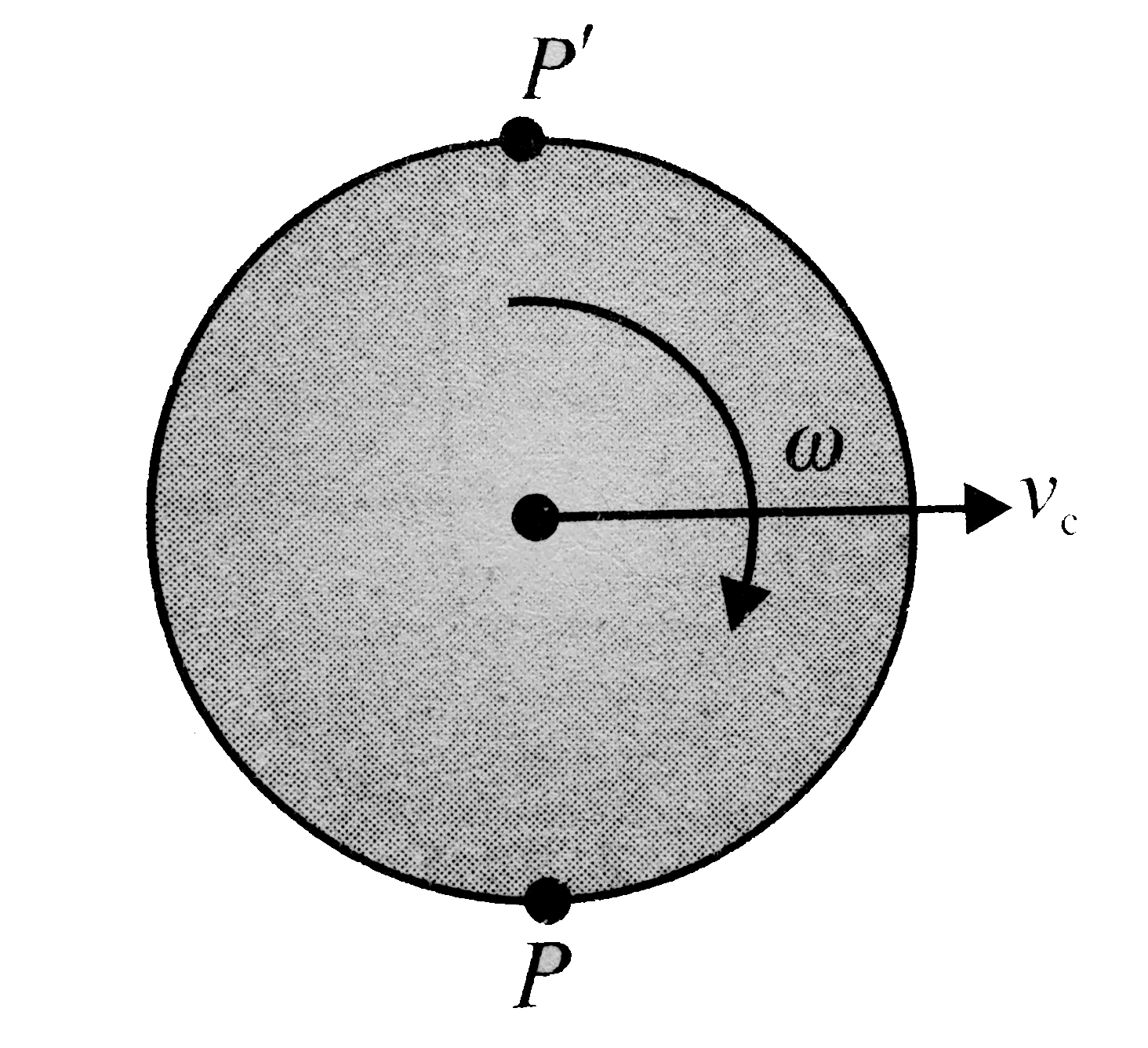 Aon point PBon point P'Cinside the sphereDoutside the sphere
Aon point PBon point P'Cinside the sphereDoutside the sphereA sphere is moving on a smooth surface with linear speed v0 and angular velocity ω0. It finds a rough inclined surface and it starts climbing up:
 Aif v0>Rω0 friction force will act downwardsBif v0<Rω0, frictio force will act upwardsCif v0=Rω0 no friction force will actDif all above case friction will act upwards
Aif v0>Rω0 friction force will act downwardsBif v0<Rω0, frictio force will act upwardsCif v0=Rω0 no friction force will actDif all above case friction will act upwards
A sphere of mass M and radius r shown in the figure on a rough horizontal plane. At some instant it has translational velocity v0, and rotational velocity about centre v0/2r. The percentage change of translational velocity after the sphere start pure rolling:

View SolutionA uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.

Disc will certainly come back to its intial position if
View SolutionA uniform circular disc of radius r . 1placed on a rough horizontal plane has initial velocity v0 and an angular velocity ω0 as shown. The disc comes to rest after moving some distance in the direction of motion. Then
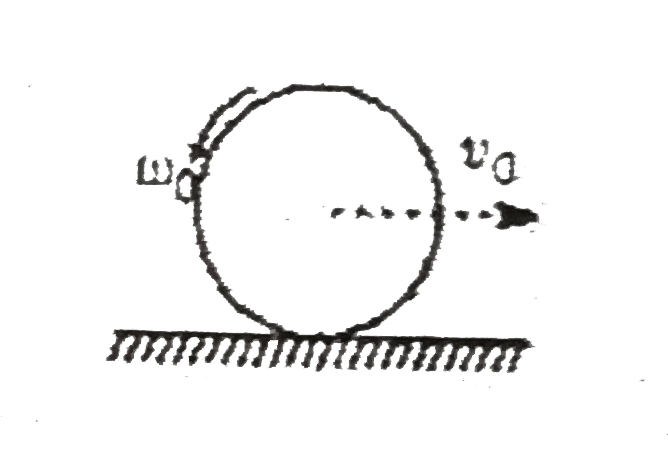
View SolutionA solid sphere is set into motion on a rough horizontal surface with a linear velocity v in the forward direction and an angular velocity v/R in the anticlockwise direction as shown in the figure. Find the linear speed of the sphere, when it stops rotating.

View SolutionA particle moves with initial velocity v0 and retardation αv, where v is velocity at any instant t. Then the particle
View Solution
