Let V and E be the gravitational potential field. Then select the correct alternative (s)
the plot of E against r (distance from centre) is discontinuous for a spherical shell
the plot of V against r is continous for a spherical shell
the plot of E against r is discontinuous for a solid sphere
the plot of V against r is continuous for a solid sphere
The correct Answer is:A, B, D
To solve the problem regarding the gravitational potential field V and the gravitational field E, we need to analyze the behavior of these fields for both a spherical shell and a solid sphere.
1. Understanding Gravitational Field E and Potential V:
- The gravitational field E is defined as the force per unit mass experienced by a small test mass placed in the field.
- The gravitational potential V at a point is defined as the work done in bringing a unit mass from infinity to that point without any acceleration.
2. Behavior of E and V for a Spherical Shell:
- Inside the Spherical Shell:
- The gravitational field E inside a spherical shell is zero.
- The gravitational potential V is constant and equal to the potential on the surface of the shell.
- Outside the Spherical Shell:
- The gravitational field E behaves as if all the mass were concentrated at the center, following E=GMr2.
- The gravitational potential V decreases with distance and follows V=−GMr.
3. Behavior of E and V for a Solid Sphere:
- Inside the Solid Sphere:
- The gravitational field E increases linearly with distance from the center, given by E=GMR3r where r is the distance from the center.
- The gravitational potential V is given by V=−GM2R+GMR3r2, which is continuous and has a maximum at the center.
- Outside the Solid Sphere:
- Similar to the shell, the gravitational field E behaves as E=GMr2.
- The gravitational potential V behaves as V=−GMr.
4. Analyzing the Plots:
- For the spherical shell:
- E is discontinuous at the surface (it jumps from 0 to a non-zero value).
- V is continuous across the surface.
- For the solid sphere:
- E is continuous throughout.
- V is also continuous throughout.
5. Selecting the Correct Alternatives:
- The correct statements based on the analysis are:
- The plot of E against R for a spherical shell is discontinuous.
- The plot of V against R is continuous for a spherical shell.
- The plot of E against R for a solid sphere is continuous.
- The plot of V against R is continuous for a solid sphere.
Conclusion:
The correct alternatives are:
- The plot of E against R for a spherical shell is discontinuous.
- The plot of V against R is continuous for a spherical shell.
- The plot of V against R is continuous for a solid sphere.
- The gravitational field E is defined as the force per unit mass experienced by a small test mass placed in the field.
- The gravitational potential V at a point is defined as the work done in bringing a unit mass from infinity to that point without any acceleration.
- Inside the Spherical Shell:
- The gravitational field E inside a spherical shell is zero.
- The gravitational potential V is constant and equal to the potential on the surface of the shell.
- Outside the Spherical Shell:
- The gravitational field E behaves as if all the mass were concentrated at the center, following E=GMr2.
- The gravitational potential V decreases with distance and follows V=−GMr.
- Inside the Solid Sphere:
- The gravitational field E increases linearly with distance from the center, given by E=GMR3r where r is the distance from the center.
- The gravitational potential V is given by V=−GM2R+GMR3r2, which is continuous and has a maximum at the center.
- Outside the Solid Sphere:
- Similar to the shell, the gravitational field E behaves as E=GMr2.
- The gravitational potential V behaves as V=−GMr.
- For the spherical shell:
- E is discontinuous at the surface (it jumps from 0 to a non-zero value).
- V is continuous across the surface.
- For the solid sphere:
- E is continuous throughout.
- V is also continuous throughout.
- The correct statements based on the analysis are:
- The plot of E against R for a spherical shell is discontinuous.
- The plot of V against R is continuous for a spherical shell.
- The plot of E against R for a solid sphere is continuous.
- The plot of V against R is continuous for a solid sphere.
The correct alternatives are:
- The plot of E against R for a spherical shell is discontinuous.
- The plot of V against R is continuous for a spherical shell.
- The plot of V against R is continuous for a solid sphere.
Topper's Solved these Questions
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Assigment problems (Objective) (level-I) Assertion & Reasoning type
2 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based
61 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
Similar Questions
Let V and E denote the gravitational potential and gravitational field at a point. Then, match the following columns
Column-IColumn-II(A)E=0,V=0(p)At centre of spherical shell(B)E≠0,V=0(q)At centre of solid sphere(C)V≠0,E=0(r)At centre of circular ring(D)V≠0,E≠0(s)At cetre of two point masses of equal magnitude(t)None
View SolutionLet VG and EG denote gravitational potential and field respectively, then choose the wrong statement.
View Solution
Knowledge Check
Select the correct alternatives :
AWork done by kinetic friction on a body always results in a loss of its kinetic energy.BWork done on a body, in the motion of that body over a close loop is zero for every force in nature.CTotal mechanical energy of a system is always conserved no matter what type of internal and ecternal forces on the body are present.DWhen total work done by a conservative force on the system is positive then the potential energy associated with this force decreases.Select the incorrect alternatives(s):
Ahas a fixed valueBmay be zeroCmay be infiniteDmay be negativeFor the given circuit, select the correct alternative(s)
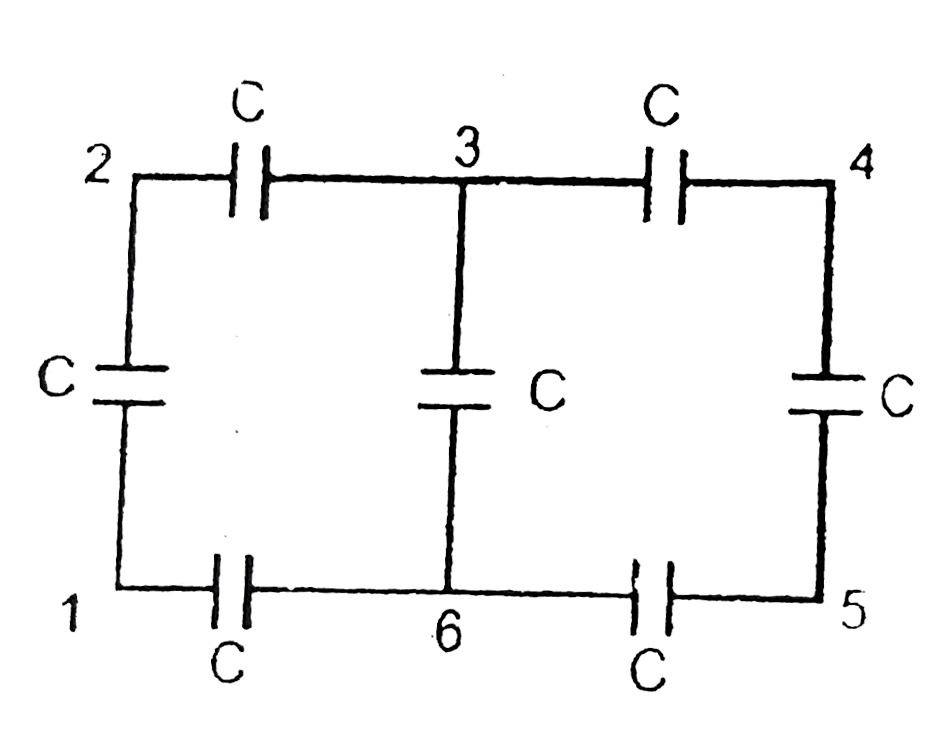 AThe equivalent capacitance between points 1&2is15C11BThe equivalent capacitance between poits 3&6is5C3CThe equivalent capacitance between points 1&3is15C14DThe equivalent capacitance between points 3&5is14C15
AThe equivalent capacitance between points 1&2is15C11BThe equivalent capacitance between poits 3&6is5C3CThe equivalent capacitance between points 1&3is15C14DThe equivalent capacitance between points 3&5is14C15
The S.I. unit of gravitational potential is
View SolutionLet VG and EG denote gravitational potential and field respectively, then choose the wrong statement.
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.
View SolutionLet V and E denote the gravitational potential and gravitational field at a point. It is possile to have
View Solution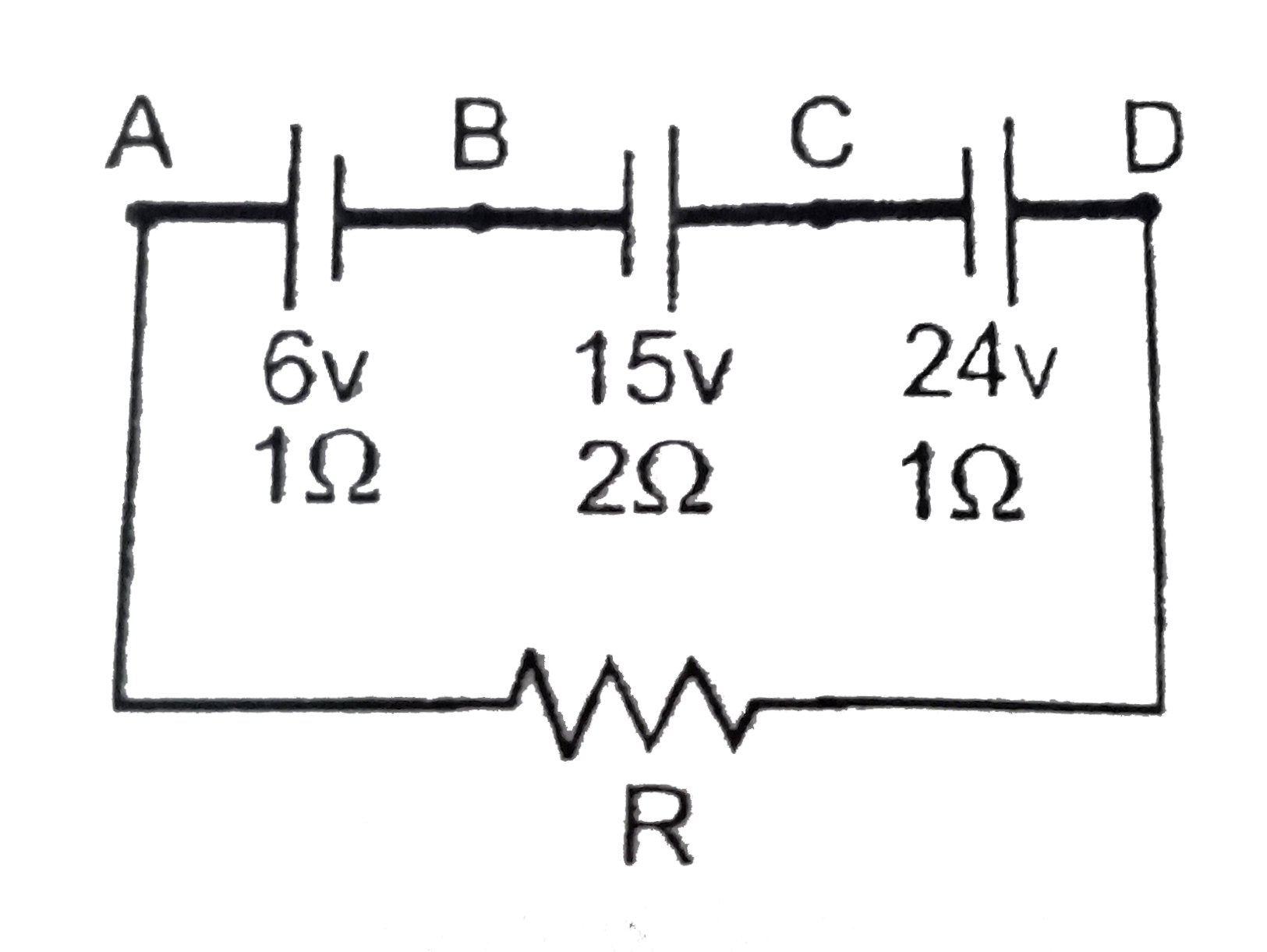
In the given circuit potential of the point A is 9 V higher than potential of the point B. Choose correct alternative (s)
View Solution
