Two small satellies move in a circular orbits around the earth, at disatnce r and (r+dr) from the centre of the earth. Their time periods of rotation ate T and T+dT(Δr<<r,ΔT<<T). Then
ΔT=32TΔrr
ΔT=−32TΔrr
ΔT=23TΔrr
ΔT=TΔrr
The correct Answer is:B
T2∝r3 or T2=cr3
⇒2TΔT=3cr2Δr
On dividing
2TΔTT2=3cr2Δrcr3
⇒ΔR=32TΔrr
Topper's Solved these Questions
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Comprehension
13 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Assertion & Reasoning type
1 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Solved problem (Subjective)
10 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based
61 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
Similar Questions
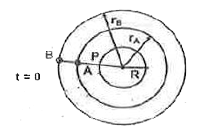
Two satellite A and B are travelling in the same plane and same sense in circular orbit around the earth at an atitude rA and rB from the centre of the earth respectively. If at time t=0 the satellite are aligned as shown in the figure, knowing that the radius of the earth R. Determine the time at which again the satellite will be aligned as they were at t=0
View SolutionA geostationary satellite is orbiting the earth at a height of 6R above the surface oof earth where R is the radius of the earth .The time period of another satellite at a distance of 3.5R from the centre of the earth is ….. hours.
View Solution
Knowledge Check
Two small satellies move in a circular orbits around the earth, at disatnce r and (r+dr) from the centre of the earth. Their time periods of rotation ate T and T+dT(Δr<<br,ΔT<<T). Then
AΔT=32TΔrrBΔT=−32TΔrrCΔT=23TΔrrDΔT=TΔrrTwo small satellites are moving in circular orbits around the earth at a distance R and R+ΔR from the centre of the earth. If their time period of rotation are T and T+ΔT respectively, then
AΔT=TΔRRBΔT=3TΔRRCΔT=32TΔRRDΔT=23TΔRRTwo small satellites are moving in circular orbits around the earth at a distance R and R+ΔR from the centre of the earth. If their time period of rotation are T and T+ΔT respectively, then
AΔT=TΔRRBΔT=3TΔRRCΔ=32TΔRRDΔT=23TΔRR
Two satellites S and S' revolve around the earth at distance 3R and 6R from the centre of the earth. Their periods of revolution will be in the ratio
View SolutionThe time period of a satellite in a circular orbit around the earth is T . The kinetic energy of the satellite is proportional to T−n . Then, n is equal to :
View SolutionA satellite moving in a circular path of radius r around earth has a time period T. If its radius slightly increases by 4%, then percentage change in its time period is
View SolutionA satellite of mass is in a stable circular orbit around the earth at an altitude of about 100 km. If M is the mass of the earth, R its radius and g the acceleration due to gravity, then the time period T of the revolution of the satellite is
View SolutionA satellite is revolving round the earth in an orbit of radius r with time period T. If the satellite is revolving round the earth in an orbit of radius r+Δr(Δr<<r) with time period T+ΔT(ΔT<<T) then.
View Solution
