The potential energy of a particle is determined by the expression U=α(x2+y2), where α is a positive constant. The particle begins to move from a point with coordinates (3,3), only under the action of potential field force. Then its kinetic energy T at the instant when the particle is at a point with the coordinates (1,1) is
The correct Answer is:8
Step by step video, text & image solution for The potential energy of a particle is determined by the expression U=alpha(x^2+y^2), where alpha is a positive constant. The particle begins to move from a point with coordinates (3, 3), only under the action of potential field force. Then its kinetic energy T at the instant when the particle is at a point with the coordinates (1,1) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - MATRIX MATCH TYPE
6 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - Exercise
16 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-I)
7 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
The potential energy of a particle is determined by the expression U=α(x2+y2), where α is a positive constant. The particle begins to move from a point with the co-ordinates (3, 3) only under the action of potential fields force. When it reaches the point (1, 1) its kinetic energy is 4Kα. Find the value of K.
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View Solution
Knowledge Check
The potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
A−3kB+3kCkDNone of theseThe potential energy of a point particle is given by the expression V(x)=−αx+βsin(x/γ). A dimensionless combination of the constant α,β and γ is–
Aα/βγBα2/βγCγ/αβDαγ/βThe potential energy of a particle in a force field is:
U=Ar2−Br,. Where A and B are positive
constants and r is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle isAabBbaC2abD2ba
The potential energy of a particle in a conservative field is U=ar3−br2 where a and b are positive constants and r is the distance of particle from the centre of field. For equilibrium, the value of r is
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x)J. The equilibrium position of the particle is at x m. The value of 10 x will be
View SolutionFor a particle moving under the action of a variable force, kinetic energy (k) varsus position (x) graph is given, then
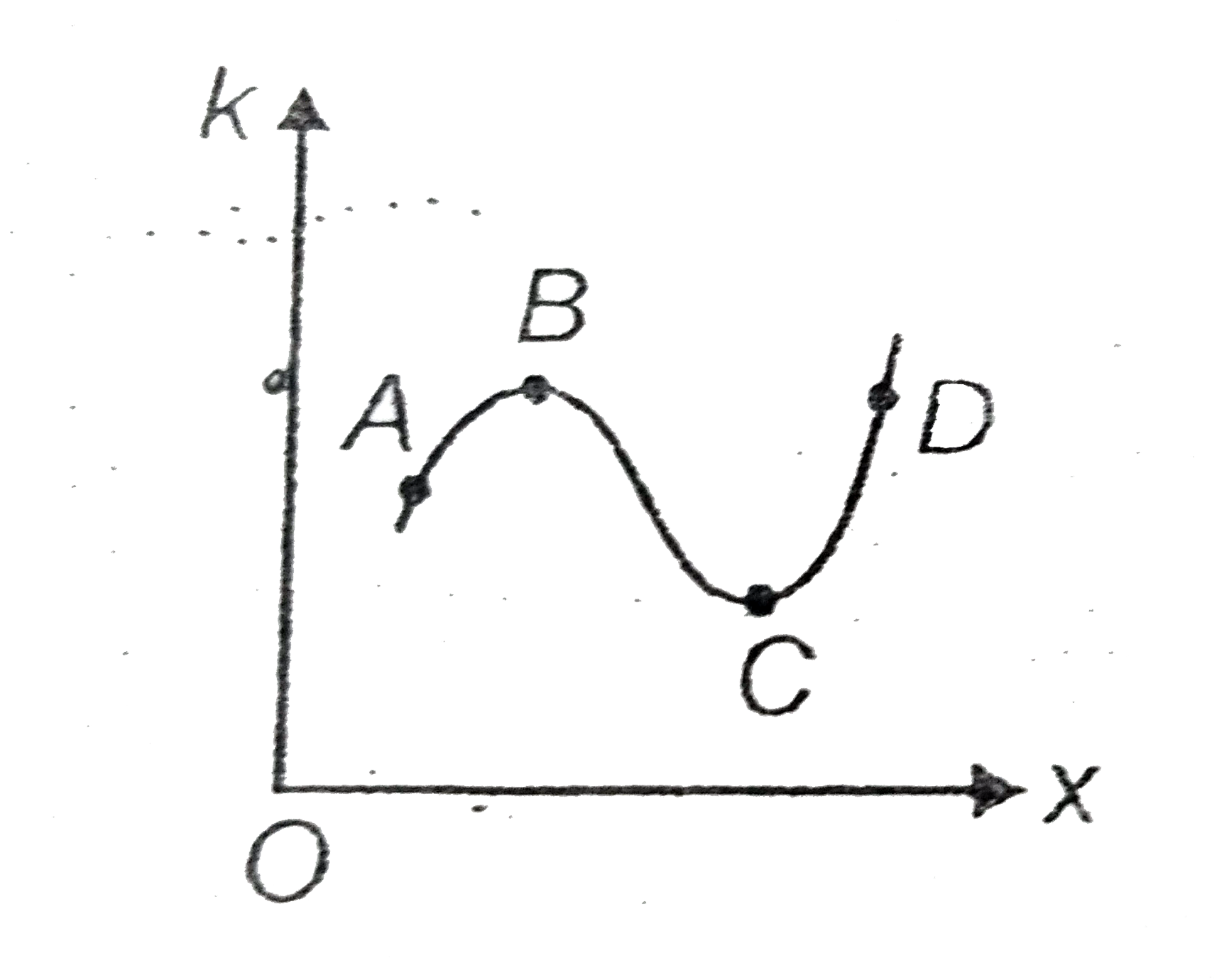
View SolutionThe potential energy of a particle in a certain field has the form U=a/r2−b/r, where a and b are positive constants, r is the distance from the centre of the field. Find:
(a) the value of r0 corresponding to the equilibrium position of the particle, examine where this position is steady,
(b) the maximum magnitude of the attraction force, draw the plots U(r) and Fr(r) (the projections of the force on the radius vector r).
View SolutionPotential energy of a particle at position x is given by U=x2−5x. Which of the following is equilibrium position of the particle?
View Solution
