A small ball is suspended from point O by a thread of length l. A nail is driven into the wall at a distance of l/2 below O, at A . The ball is drawn aside so that the thread taken up a horizontal position at the level of point O and then released. Find
(a) A what point of the ball's trajectory, will the tension in the thread disappear?
(b) What will be the highest point to which it will rise?
To solve the problem step by step, we will break it down into two parts as per the question:
Part (a): Finding the point where the tension in the thread disappears.
1. Understanding the Setup:
- A small ball is suspended from point O by a thread of length l.
- A nail is driven into the wall at point A, which is l2 below O.
- The ball is drawn aside to a horizontal position and then released.
2. Identifying Forces:
- When the ball is at an angle θ from the vertical, the forces acting on it are:
- The weight of the ball mg acting downward.
- The tension T in the thread acting along the thread.
3. Applying the Condition for Zero Tension:
- The tension in the thread will disappear when the centripetal force required for circular motion is provided entirely by the component of the gravitational force acting towards the center of the circular path.
- At this point, the equation can be written as:
T+mgcosθ=mv2l2
- Setting T=0 gives us:
mgcosθ=mv2l2
- Simplifying, we find:
gcosθ=2v2l
4. Using Energy Conservation:
- When the ball is released from the horizontal position, it has potential energy mgl and no kinetic energy.
- At the lowest point, all potential energy converts to kinetic energy:
mgl=12mv2
- Thus, v2=2gl.
5. Substituting Back:
- Substituting v2 into the earlier equation:
gcosθ=2(2gl)l
- This simplifies to:
gcosθ=4g
- Therefore, cosθ=42=2, which is not possible.
6. Finding the Correct Angle:
- We need to find where the ball will lose tension. The angle θ can be found using the condition that the ball will not complete the circular motion.
- The angle at which tension becomes zero can be derived from the geometry of the situation, leading to:
cosθ=23
- Hence, the angle θ where tension becomes zero is:
θ=cos−1(23)
Part (b): Finding the highest point to which the ball will rise.
1. Projectile Motion After Losing Tension:
- Once the tension disappears, the ball will move in a projectile motion.
- The velocity at the point where tension is zero can be calculated using:
v2=2gl
- The height reached in projectile motion can be calculated using the formula:
h=v2sin2θ2g
2. Calculating the Height:
- We substitute v2 and sinθ:
h=(2gl)sin2θ2g=lsin2θ
- From the earlier calculation, we know:
sin2θ=1−cos2θ=1−(23)2=1−49=59
- Therefore:
h=l⋅59=5l9
3. Total Height:
- The total height from the lowest point (A) to the maximum height reached is:
H=l2+5l9=9l+10l18=19l18
Final Answers:
- (a) The tension in the thread disappears at an angle θ=cos−1(23).
- (b) The highest point to which the ball will rise is 19l18.
- A small ball is suspended from point O by a thread of length l.
- A nail is driven into the wall at point A, which is l2 below O.
- The ball is drawn aside to a horizontal position and then released.
- When the ball is at an angle θ from the vertical, the forces acting on it are:
- The weight of the ball mg acting downward.
- The tension T in the thread acting along the thread.
- The tension in the thread will disappear when the centripetal force required for circular motion is provided entirely by the component of the gravitational force acting towards the center of the circular path.
- At this point, the equation can be written as:
T+mgcosθ=mv2l2
- Setting T=0 gives us:
mgcosθ=mv2l2
- Simplifying, we find:
gcosθ=2v2l
- When the ball is released from the horizontal position, it has potential energy mgl and no kinetic energy.
- At the lowest point, all potential energy converts to kinetic energy:
mgl=12mv2
- Thus, v2=2gl.
- Substituting v2 into the earlier equation:
gcosθ=2(2gl)l
- This simplifies to:
gcosθ=4g
- Therefore, cosθ=42=2, which is not possible.
- We need to find where the ball will lose tension. The angle θ can be found using the condition that the ball will not complete the circular motion.
- The angle at which tension becomes zero can be derived from the geometry of the situation, leading to:
cosθ=23
- Hence, the angle θ where tension becomes zero is:
θ=cos−1(23)
- Once the tension disappears, the ball will move in a projectile motion.
- The velocity at the point where tension is zero can be calculated using:
v2=2gl
- The height reached in projectile motion can be calculated using the formula:
h=v2sin2θ2g
- We substitute v2 and sinθ:
h=(2gl)sin2θ2g=lsin2θ
- From the earlier calculation, we know:
sin2θ=1−cos2θ=1−(23)2=1−49=59
- Therefore:
h=l⋅59=5l9
- The total height from the lowest point (A) to the maximum height reached is:
H=l2+5l9=9l+10l18=19l18
- (a) The tension in the thread disappears at an angle θ=cos−1(23).
- (b) The highest point to which the ball will rise is 19l18.
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:SOLVED PROBLEMS (SUBJECTIVE )
Explore 8 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:SOLVED PROBLEMS ( OBJECTIVE)
Explore 18 Videos
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
Similar Questions
A small ball is suspended from point O by a thread of length l. A nail is driven into the wall at a distance of l/2 below O, at A. The ball is drawn aside so that the thread takes up a horizontal position at the level of point O and then released. Find
a. At what angle from the vertical of the ball's trajectory, will the tension in the thread disappear?
b. What will be the highest point from the lowermost point of circular track, to which it will rise?
View SolutionA simple pendulum consists of a ball of mass m connected to a string of length L. The ball is pulled aside so that the string makes an angle of 53∘ with the verticle and is released. Find the ratio of the minumum and the tension in the string.
View Solution
Knowledge Check
A small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω.
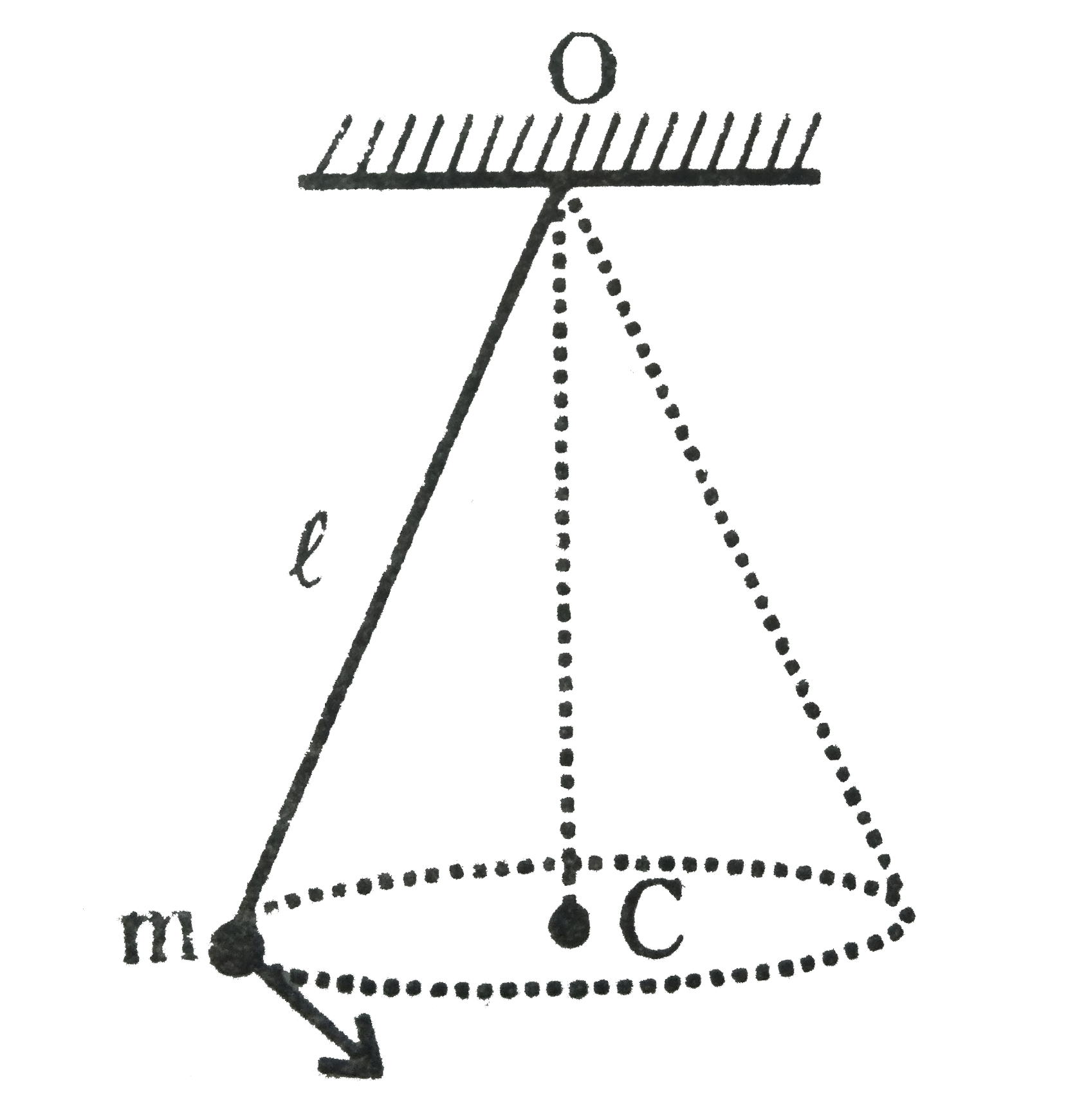 .Alinear momentum of system (ball + rod) is conservedBangular momentum about C is conservedCkinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collisionDlinear momentum of ball is conserved
.Alinear momentum of system (ball + rod) is conservedBangular momentum about C is conservedCkinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collisionDlinear momentum of ball is conservedA small sphere of mass m suspended by a thread is first taken a side so that the thread forms the right angle with the vertical and then released, then
ATotal acceleration of sphere as a function of θ measured from the vertical is g√1+3cos3θBThread tension as a function of θ measured from the vertical is T=3mgcosθCThe angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally is cos−11/√3.DThe thread tension at the moment when the vertical component of the sphere's velocity is maximum will be mg.A spere is suspended by a thread of length l. What minimum horizontal velocity has to be imparted to the ball for it to reach the height of the suspension?
AglB2glC√glD√2gl
A small ball is suspended from a point O by a light thread of length l. Then the ball is drawn aside so that thread deviates through an angle θ from the vertical and set in motion in a horizontal direction at right angles to the vertical plane in which the thread is located. What is the initial velocity that has to be imparted to the ball so that it could deviate through the maximum angle π/2 in the process of motion?
View SolutionA small ball is suspended from a fixed point 'O' by means of a light and inextensible string of length 'l'. The ball is first taken aside such that string becomes horizontal and then released from rest. At the borrom it collides with a fixed obstacle. The co-efficient of restitution is 'e'. Find the maximum angular deflection of the string after nth collision.
View SolutionA ball of mass m is suspended by a thread of length l. With what minimum velocity has the point of suspension to be shifted in the horizontal direction for the ball to move along the circle about that point? What will be the tension of the thread at the moment it will be passing the horizontal position?
View SolutionA weight is suspended from a thread of length l. What is the initial speed that has to be imparted to it at the lowest point to make it complete a full revolution? The mass of the thread is to be neglected.
View SolutionA spere is suspended by a thread of length l. What minimum horizontal velocity has to be imparted to the ball for it to reach the height of the suspension?
View Solution

