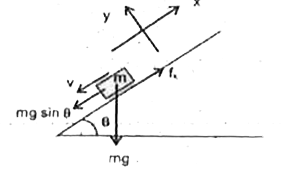
A block of mass m is moving down with constant velocity along an inclined plane of inclination θ. What is the work done by external force in pulling the block along the inclined plane through a height h with constant velocity?
Since the block moves down along the inclined plane with constant velocity , its net acceleration is zero. Therefore the net external force acting on the block is zero.
⇒ΣFx=0 and ΣFy=0
⇒mgsinθ−fx=0,
where fx= kinetic friction developed at the interface of the block and the inclined plane (since the block is sliding).
⇒fk=mgsinθ ...(1)
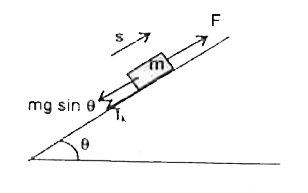
Let the applied force F be parallel to the inclined plane. When it pulls the block up, kinetic friction acts down to oppose the relative motion. The work done by the force to displace the block through a distance l along the inclined plane is given as
W=→F.→s=Fs=Fl
where, l=hcosecθ
⇒W=Fhcosecθ...(2)
Since the block slides up with constant velocity, the net acceleration, therefore the net force acting on the block,
ΣFx=0 and ΣFy=0
⇒F−mgsinθ−fk=0 ...(3)
Using (1) and (3)
F=2mgsinθ ...(4)
Using (2) and (3), we obtain
W=2mgh
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - SOLVED PROBLEMS (SUBJECTIVE )
8 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - SOLVED PROBLEMS ( OBJECTIVE)
18 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
A block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

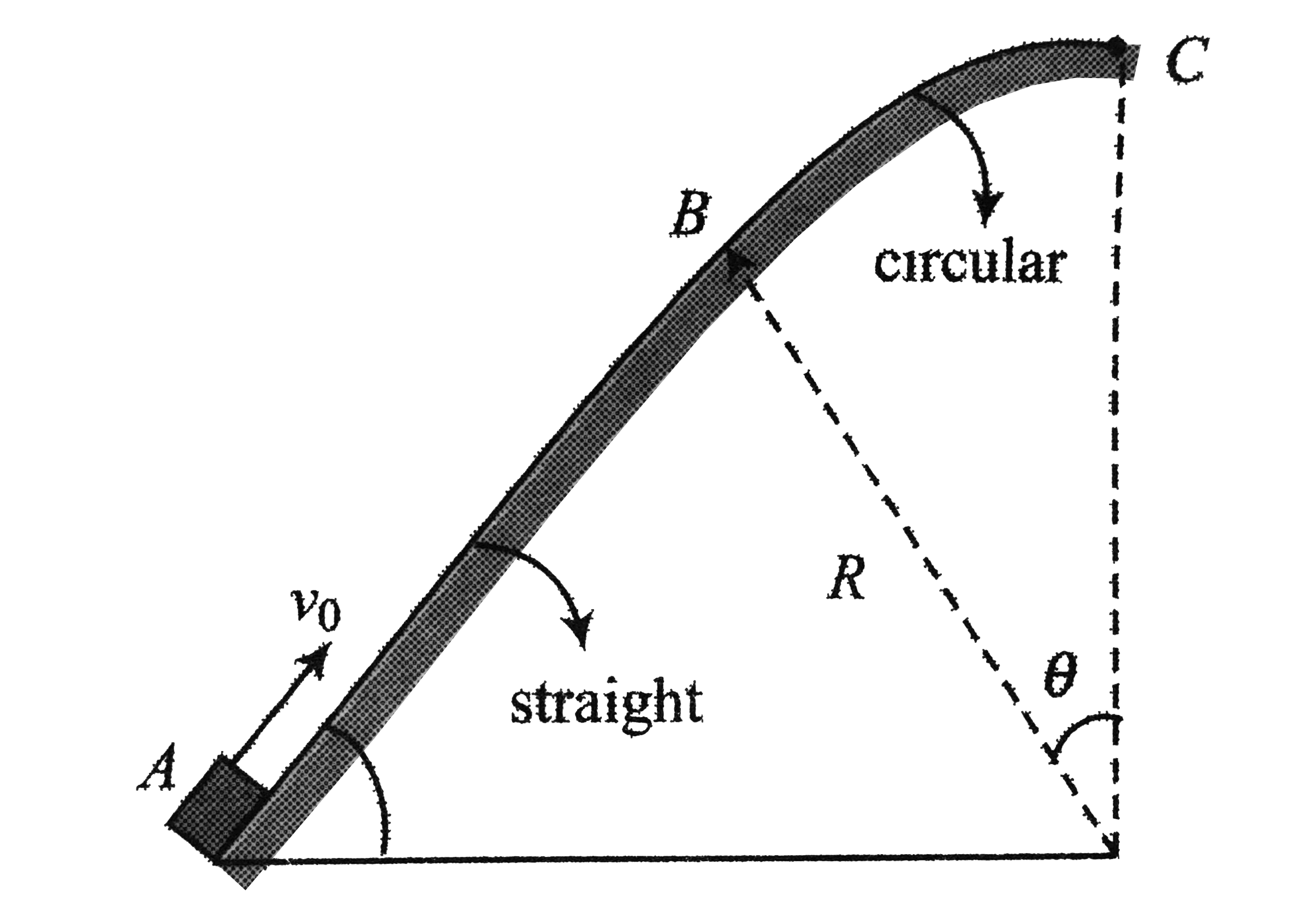
View SolutionA block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
View Solution
Knowledge Check
A block of mas m begins to slide down on an inclined plane of inclination θ. The force of friction will be
AmgBmgcosθCmgsinθDmgtanθA block of mass m is placed on a rough inclined plane of inclination θ kept on the floor of the lift. The coefficient of friction between the block and the inclined plane is μ. With what acceleration will the block slide down the inclined plane when the lift falls freely ?
AZeroBgsinθ−μgcosθCgsinθ−μgcosθDNone of theseA block of mass m slides down with uniform speed on an inclined plane having inclination θ If the coefcient of friction between the inclined plane and the block is then the contact force between them is
AmgsinθBmgC√(mgsinθ)2+(μπgcosθ)2Dmgcosθ√1+μ2
A cubical block of mass M and edge a slides down a rougg inclined plane of inclination θ with a uniform velocity. The torque of the normal force on the block about its centre has magnitude.
View SolutionA drum of radius R and mass M rolls down without slipping along an inclined plane of angle θ. The frictional force
View SolutionThe velocity of a sphere rolling down an inclined plane of height h at an inclination θ with the horizontal, will be :
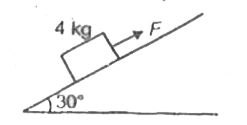
View SolutionA block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
View SolutionA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View Solution
