A particle moves in the x-y plane according to the law x=t2, y = 2t. Find:
(a) velocity and acceleration of the particle as a function of time,
(b) the speed and rate of change of speed of the particle as a function of time,
(c) the distance travelled by the particle as a function of time.
(d) the radius of curvature of the particle as a function of time.
The correct Answer is:(a) →a=2ˆi (b) 2t√t2+1 (c) sqrt(t^(2)+1)+In[t+sqrt(t^(2)+1)](d)2(t^(2)+1)^(3//2)
Step by step video, text & image solution for A particle moves in the x-y plane according to the law x=t^(2), y = 2t. Find: (a) velocity and acceleration of the particle as a function of time, (b) the speed and rate of change of speed of the particle as a function of time, (c) the distance travelled by the particle as a function of time. (d) the radius of curvature of the particle as a function of time. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I
Explore 45 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I (ASSERTION REASONING TYPE)
Explore 2 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-I (Numerical)
Explore 8 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
Similar Questions
The position x of a particle varies with time t according to the relation x=t3+3t2+2t. Find the velocity and acceleration as functions of time.
View SolutionThe acceleration of a particle is increasing linearly with time t as bt .The particle starts from the origin with an initial velocity v_(0) The distance travelled by the particle in time t will be
View Solution
Knowledge Check
A particle moves in x-y plane according to equations x=4t2+5t and 6y=5t The acceleration of the particle must be
A8m/sec2B12m/sec2C14m/sec2Dnone of the aboveA particle moves a distance x in time t according to equation x2=1+t2 . The acceleration of the particle is
A1x3B1x−1x2C−tx2D1x−t2x3Figure shows the graph of acceleration of particle as a function of time. The maximum speed of the particle is (particle starts from rest).
 A7m/sB8m/sC4m/sD16m/s
A7m/sB8m/sC4m/sD16m/s
A particle move a distance x in time t according to equation x=(t+5)−1. The acceleration of particle is alphaortional to.
View SolutionA particle move a distance x in time t according to equation x=(t+5)−1. The acceleration of particle is alphaortional to.
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
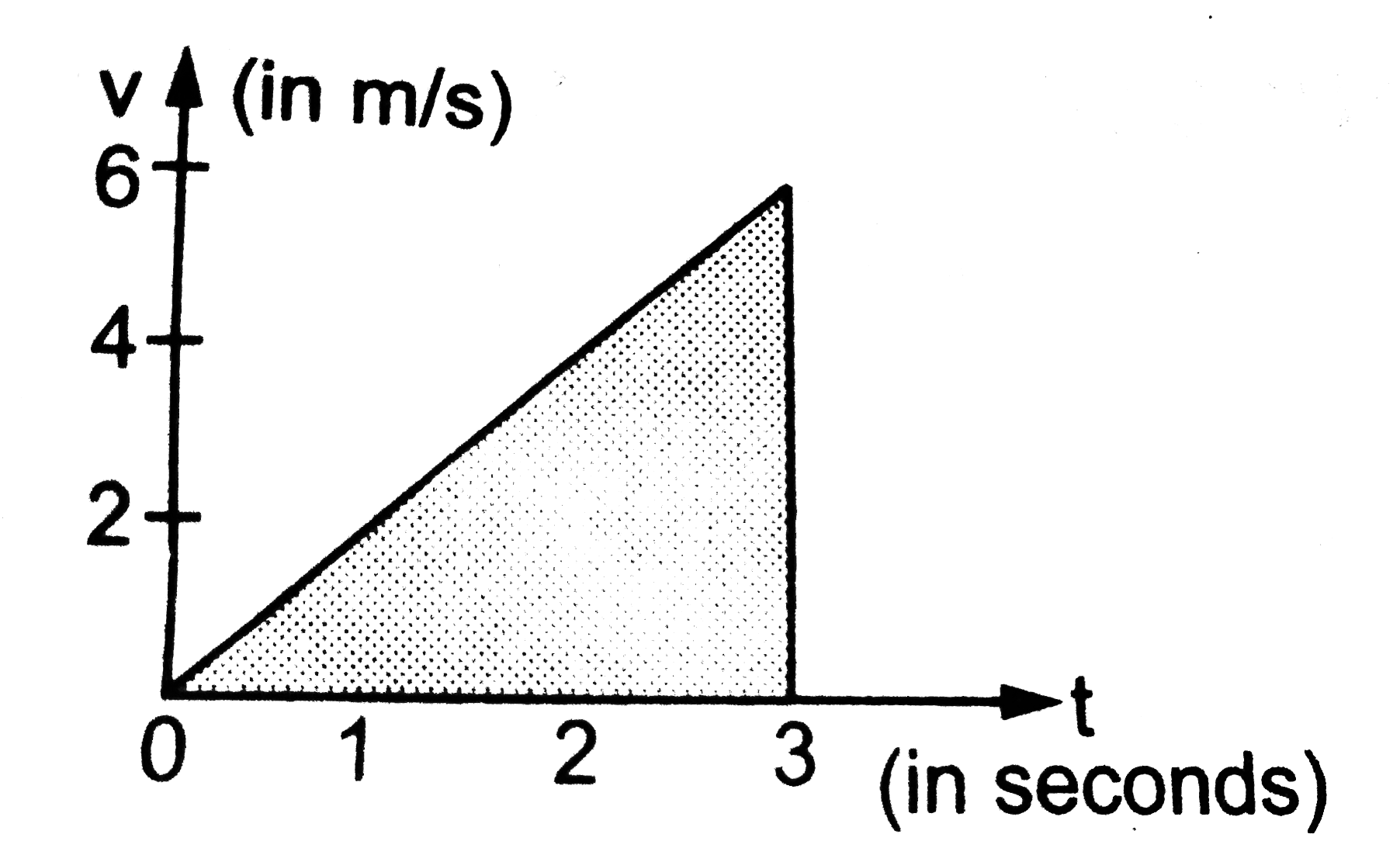
View SolutionThe displacement of a particle is s=(a+bt)6, where a and b are constants. Find acceleration of the particle as a function of time.
View SolutionA particle move a distance x in time t according to equation x=(t+5)−1. The acceleration of particle is alphaortional to.
View Solution