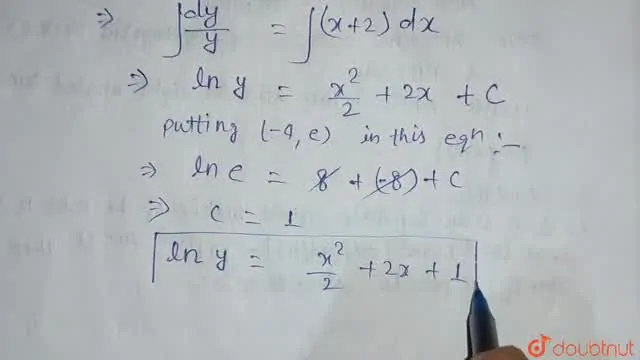A curve is such that the slope of the tangent to it at any point P is the product of ordinate of P and abscissa increased by 2. If it passes through then its equation is
Step by step video, text & image solution for A curve is such that the slope of the tangent to it at any point P is the product of ordinate of P and abscissa increased by 2. If it passes through (-4, e), then its equation is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
At any point on a curve , the slope of the tangent is equal to the sum of abscissa and the product of ordinate and abscissa of that point.If the curve passes through (0,1), then the equation of the curve is
View SolutionThe slope of the tangent to the curve at any point is reciprocal of twice the ordinate of that point. The curve passes through the point (4,3). Determine its equation.
View SolutionThe curve y=f(x) in the first quadrant is such that the y - intercept of the tangent drawn at any point P is equal to twice the ordinate of P If y=f(x) passes through Q(2,3), then the equation of the curve is
View SolutionThe curve in which the slope of the tangent at any point equal the ratio of the abscissa to the ordinate of the point is
View SolutionA curve in the first quadrant is such that the slope of OP is twice the slope of the tangent drawn at P to the curve, where O is the origin and P is any general point on the curve. If the curve passes through (4, 2), then its equation is
View SolutionThe slope of the tangent to the curve y=√9−x2 at the point where ordinate and abscissa are equal, is
View SolutionThe slope of a curve at any point is the reciprocal of twice the ordinate at that point and it passes through the point(4,3). The equation of the curve is:
View SolutionThe slope of a curve at any point is the reciprocal of twice the ordinate at that point and it passes through the point(4,3). The equation of the curve is:
View SolutionSlope of a curve at any point (x, y) on it is (4x−3). If u passes through the point (1, 3), then its equation is
View SolutionIf a curve passes through the origin and the slope of the tangent to it at any point (x, y) is x2−4x+y+8x−2, then this curve also passes through the point:
View Solution