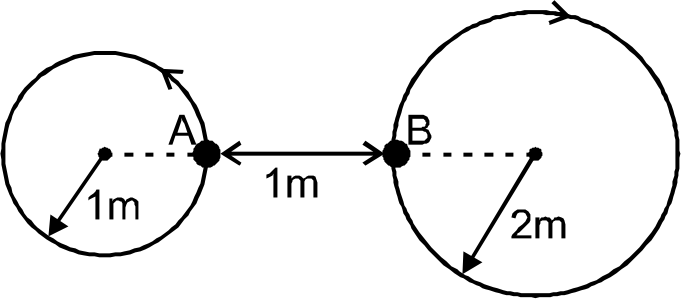
Two particles A,B are moving on two concentric circles of radii R1) and R2 with equal angular speed ω. Att=0,their positions and direction fo motion are shown in the figure :
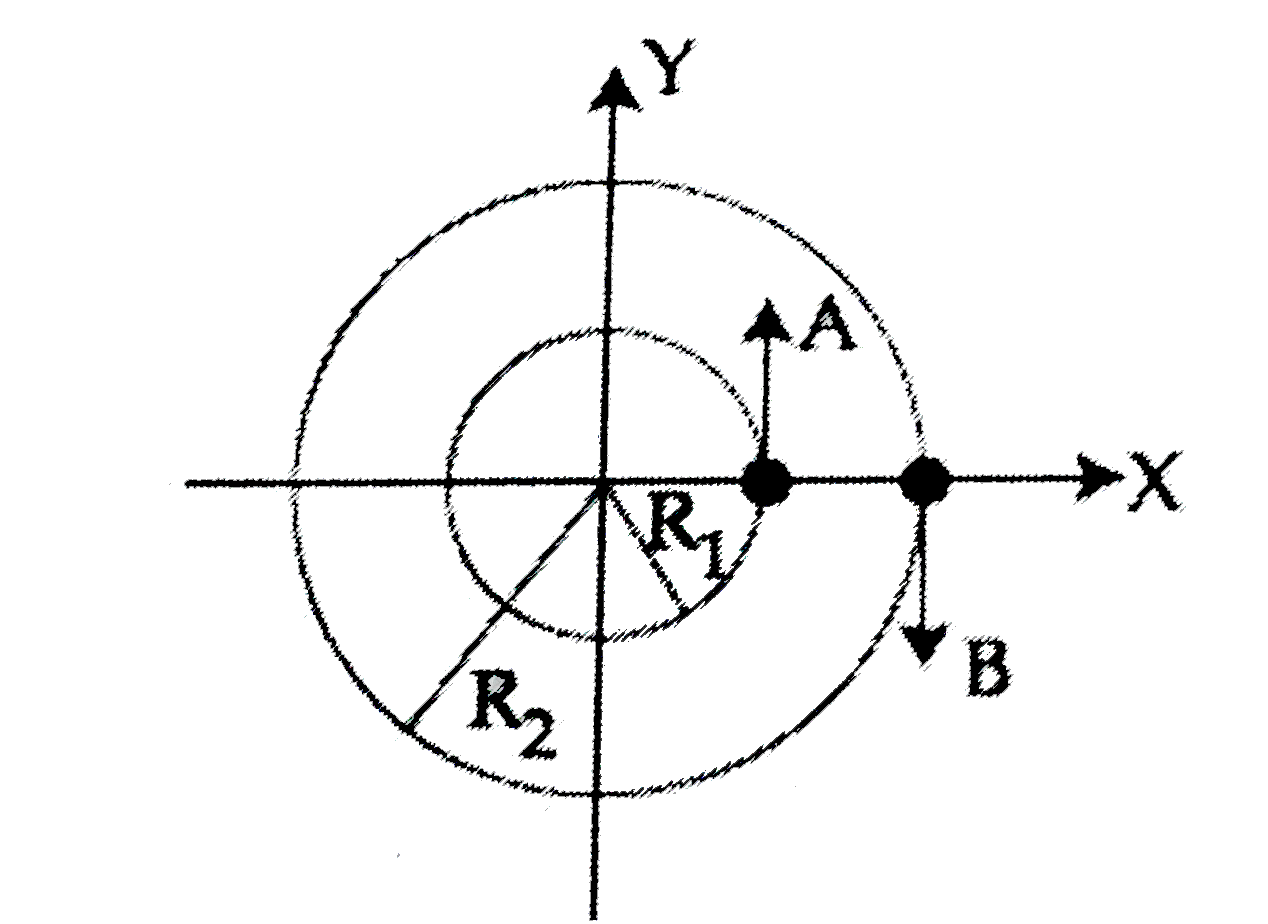
−ω(R1+R2)ˆi
ω(R1+R2)ˆi
ω(R1−R2)ˆi
ω(R2−R1)ˆi
The correct Answer is:D
Step by step video, text & image solution for Two particles A,B are moving on two concentric circles of radii R_1) and R_2 with equal angular speed omega. Att=0,their positions and direction fo motion are shown in the figure : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two particles A and B are revolving with constant angular velocity on two concentric circles of radius 1m and 2m respectively as shown in figure. The positions of the particles at t = 0 are shown in figure. The positions of the particles at t=0 are shown in figure. if mA=2kg,mB=1kg and →PA and →PB are linear momentum of the particle then what is the maximum value of ∣∣→PA+→PB∣∣ in kg-m/sec in subsequent motion of two particles.
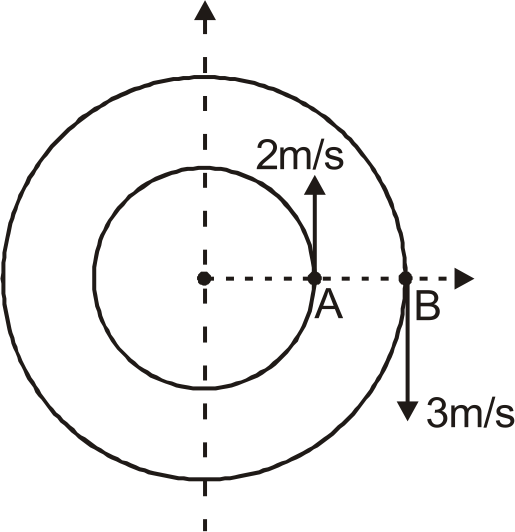
View SolutionTwo particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are θA=(π2t) and θB=(πt) respectively. here θ is in radian and t is in second. Radius of each circle is shown in diagram.
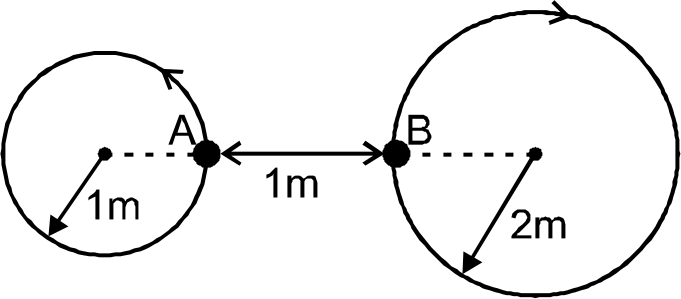
At time t=1 sec. the magnitude of acceleration of A with respect to B is
View Solution
Knowledge Check
Two particles A and B are moving in uniform circular motion in concentric circles of radii rA and rB with speed uA and uB respectively. Their time period of rotation is the same. The ratio of angular speed of a to that of B will be:
A1:1BrA:rBCυA:υBDrB:rATwo particles A and B are moving in uniform circular motion in concentric circles of radii rA and rB with speed uA and uB respectively. Their time period of rotation is the same. The ratio of angular speed of a to that of B will be:
ArA:rBBVA:VBCrB:rAD1:1Two particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are θA=(π2t) and θB=(πt) respectively. here θ is in radian and t is in second. Radius of each circle is shown in diagram.
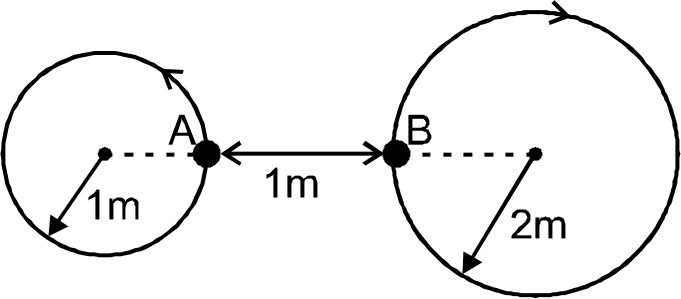
At time t=2 second, the angular velocity of the particle A with respect to the particle B isA5π rad/secB3π2 rad/secC2π3 rad/secD5π6 rad/sec
Two particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are θA=(π2t) and θB=(πt) respectively. here θ is in radian and t is in second. Radius of each circle is shown in diagram.
Find the magnitude of acceleration of A at t=1 sec
View SolutionThe capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
View SolutionTwo racing cars having masse m1andm2 move in concentric circle of radii r1andr2 respectively. If their angular speed are same , then ratio of their linear speed is
View SolutionTwo particles of masses m1andm2 are moving in concentric circle of radii r1andr2 such that their period are same. Then the ratio of their centripetal acceleration is
View SolutionTwo racing cars having masses m1 and m2 move in concentric circles of radius r1 and r2 respectively . If their angular speeds are same , then the ration of their linear speeds is
View Solution