A uniform disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is μ Fig. Now the disc is pulled with a force F as shown in the Fig. What is the maximum value of F for which the disc rolls without slipping ?


μMg
2μMg
3μMg
4μMg
The correct Answer is:c
Let a be the acceleration of the center of the mass of disc. Then Ma=F−f………(i)
If there is no slipping, angular acceleration of the disc,
α=aR
Now torque of the disc τ=Iα=Rf
or τ=(12MR2)α=Rf ∴ For a disc I=12MR2
∴(12MR2)(aR)=Rf⇒Ma=2f (using (ii))
Substituting this in Eq. (i), we get
2f=F-f or f=F3
Since, there is no slipping,
∴f≤μMg⇒F≤3μMg∴Fmax=3μMg

Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTIPSChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:Angular Momentum In Case Of Rotations About A Fixed Axis
Explore 16 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTIPSChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:Rolling Motion
Explore 16 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTIPSChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:Kinematics Of Rotational Motion About A Fixed Axis
Explore 3 Videos
- PRACTICE PAPERSBook:NCERT FINGERTIPSChapter:PRACTICE PAPERSExercise:Practice Paper 3
Explore 50 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTIPSChapter:THERMAL PROPERTIES OF MATTERExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
A unifrom disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is μ Fig. Now the disc is spulled with a force F as shown in the Fig. What is the maximum value of F for which the disc rolls without slipping ?


View SolutionA horizontal force F acts on the sphere at its centre as shown. Coefficient of friction between ground and sphere is μ. What is maximum value of F for which there is no slipping?
View Solution
Knowledge Check
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank isAF2BF4CF3D2F3A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank isAF2mB3F4mCF4mD3F2mA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
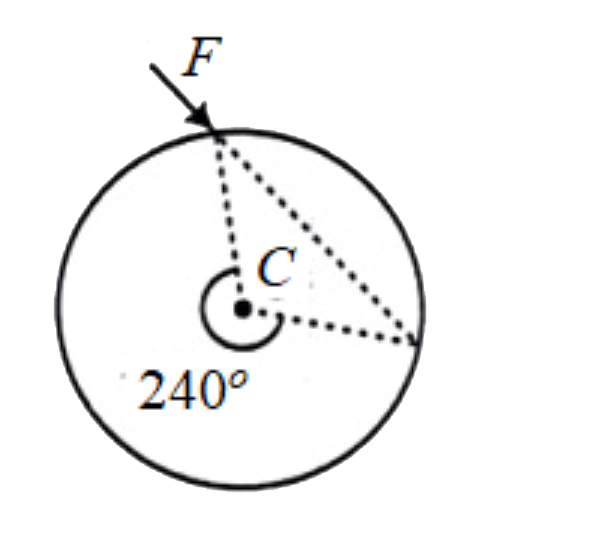 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MR
A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
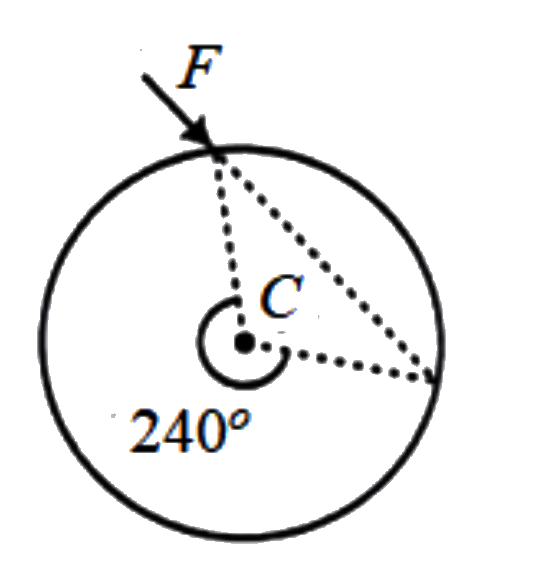
View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
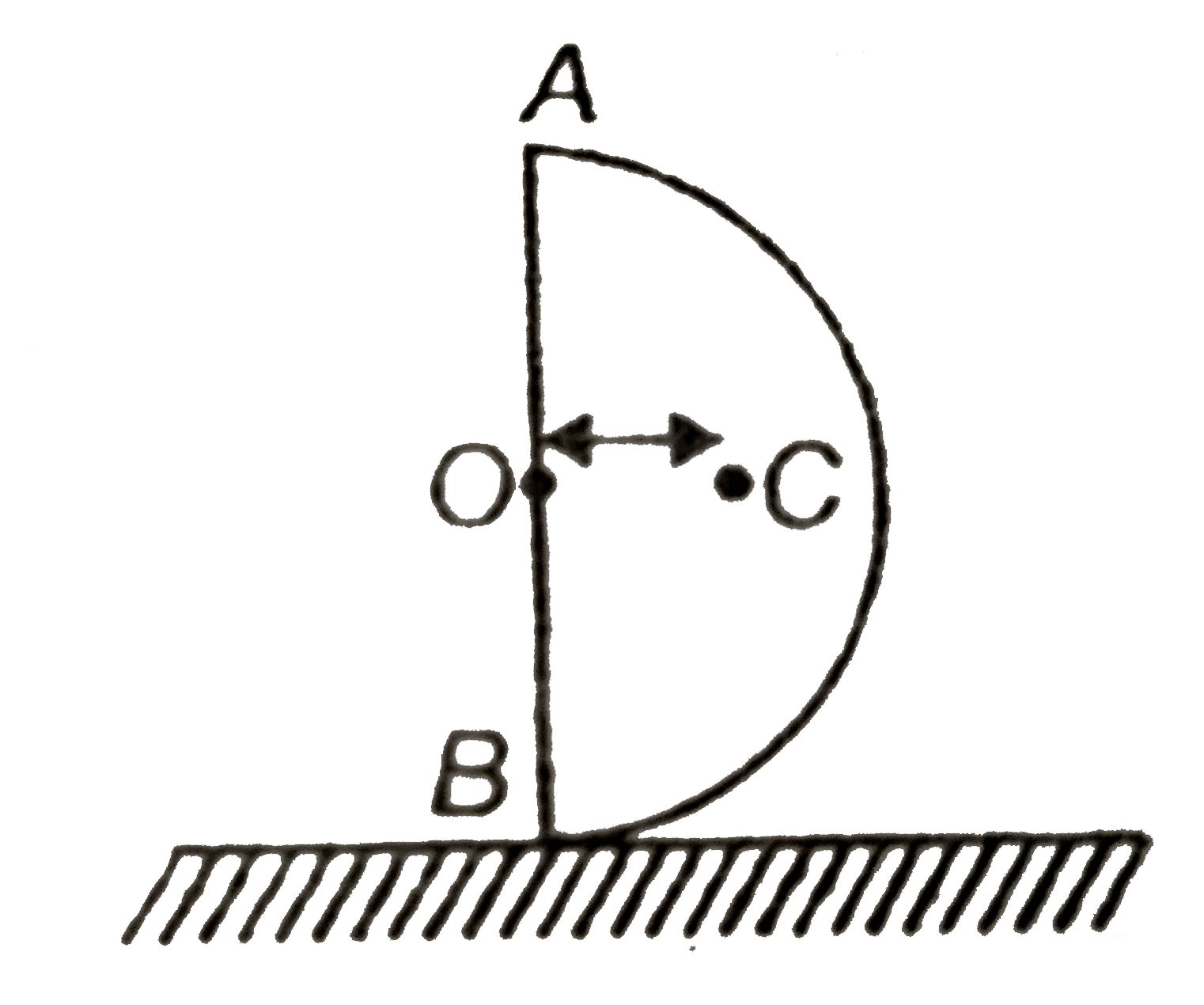
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
View SolutionA horizontal force F acts at the centre of mass of a uniform disc with mass M and radius R. The maximum value of F for which the disc can roll without slipping is kμsMg. Find k. ( μ, is coefficient of friction)
View SolutionA disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is

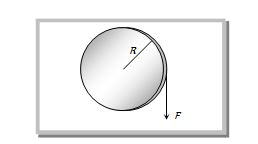
View SolutionA uniform disc of radius R and mass M can rotate on a smooth axis passing through its centre and perpendicular to its plane. A force F is applied on its rim. See fig. What is the tangential acceleration
View Solution

